Metamath-lamp Guide: User Guide (Tutorial) and Reference Manual | Metamath-lamp Guide

Metamath-lamp Guide: User Guide (Tutorial) and Reference Manual

by David A. Wheeler

Metamath-lamp (Lite Assistant for Metamath Proofs) is a proof assistant for creating formal mathematical proofs in the Metamath system. Unlike most other Metamath proof systems, such as mmj2 or metamath-exe (the first Metamath proof assistant), users of metamath-lamp can use this proof assistant without installing anything. Instead, you can start using metamath-lamp by using your web browser, including your smartphone web browser, by viewing its application page:

Metamath-lamp application page

Since the metamath-lamp tool supports Metamath, we should explain what Metamath is. Metamath is a “simple and flexible computer-processable language that supports rigorously verifying, archiving, and presenting mathematical proofs”. The underlying Metamath language is simple and not tied to any particular set of axioms; instead, axioms are defined in a database (a text file of axioms and theorems). An especially unusual trait of Metamath is that its proofs include every step, no exceptions, where each step is only an application of an axiom or a previously-proved statement. This is different from almost all other computer-verifiable proof systems, which allow statements (like “simp”, “auto”, or “blast”) that don’t show the proof steps but instead ask a computer to try to rediscover the proof steps (and often just take the computer’s word for it). Metamath’s unique approach speeds verification, improves archiving, and enables anyone to follow every proof step - from high-level math all the way down to fundamental axioms. Metamath is one of the top systems in the Formalizing 100 Theorems challenge; there’s a long list of mathematical proofs formally verified by Metamath from that list.

This Metamath-lamp Guide is both a user guide (tutorial) and a reference guide. It includes:

1. Quick start briefly introduces how to start and use metamath-lamp.
2. Sample Screenshot
3. User guide (tutorial) shows how to use the metamath-lamp tool. It covers proving 2 + 2 = 4 (2p2e4), a tour using the Explorer tab, the principle of the syllogism (syl), a proof that the reciprocal of the cotangent is tangent (reccot), creating your own examples from existing proofs, loading existing metamath-lamp proofs, and notes about Metamath databases.
4. Reference manual explains each part of the user interface, e.g., the Editor tab.
5. Future directions discusses likely future directions.
6. Help, feedback, and contributions
7. Licensing
8. Detailed table of contents
9. Authors and Reviewers

Metamath-lamp is a new proof assistant for creating Metamath proofs. As a result, it currently lacks some planned functionality such as undo/redo, full syntactic unification, and some of the automation rules included in other tools like mmj2. That said, metamath-lamp already provides useful functionality, including some automation support. It can also run directly in your web browser with no additional installation, including on a smartphone, which some may find compelling. We hope you’ll find it useful.

Metamath-lamp improves over time, so some of this guide may not exactly match what you see. If you see a difference, please let us know so we can fix this guide. This guide was written for release version 11. You can also see the guide for version 10.

The latest version of this Metamath-lamp guide is available at <https://lamp-guide.metamath.org/>.

We also have “Introduction to Metamath-lamp” tutorial videos available: part 1, part 2, part 3.

Quick start

You don’t need to install anything to run metamath-lamp, and it works on personal computers and smartphones. To start metamath-lamp, use your web browser to view the Metamath-lamp application page

To use metamath-lamp, do the following:

1. Load the proof context (the databases you’ll use and their scope).
2. Set the fundamental proof information where desired (its description, variables, and disjoints).
3. Add the goal (qed) and any (essential) hypotheses to the list of steps. Set their labels to what you want them to be in the final database.
4. Now create the proof. To do this, you add other steps and repeatedly unify them until the goal is completely proven. You can create the proof backwards from the goal, forwards towards the goal, or in whatever other order makes sense to you.
5. Get the final results using “Show completed proof”. You’d typically copy the compressed proof text into a Metamath database (which is a text file).

Throughout metamath-lamp there are various tooltips. So if you use a mouse and hover over an interactive item, the tool will often provide a brief explanation. You don’t need to memorize this guide.

We use the term “click” to mean a click with the left mouse button or a tap on a touchscreen. A short click (or short tap) lets you reveal information, toggle a display, or select some information. “Press” means pressing and releasing a key or clicking on a button.

Edits generally require a long-click by default. There are multiple ways to do a long-click. Using a mouse, you can press down on the mouse, wait a second, then release. Using a touchscreen, you can press down on the screen, wait a second, then release. With a mouse you can also use a shortcut: hold the Alt key (sometimes labelled Opt or Option instead), then click with the mouse.

Also:

• To save an edit, use the icon save (save) or press Enter (Return).
• To cancel an edit, use the icon cancel (cancel) or press Esc (Escape).
• To delete something selected, use the icon delete (delete).

Sample Screenshot

Here’s a sample screenshot to give you an idea of what using metamath-lamp looks like (proving that 2 + 2 = 4):

Screenshot of 2 + 2 = 4

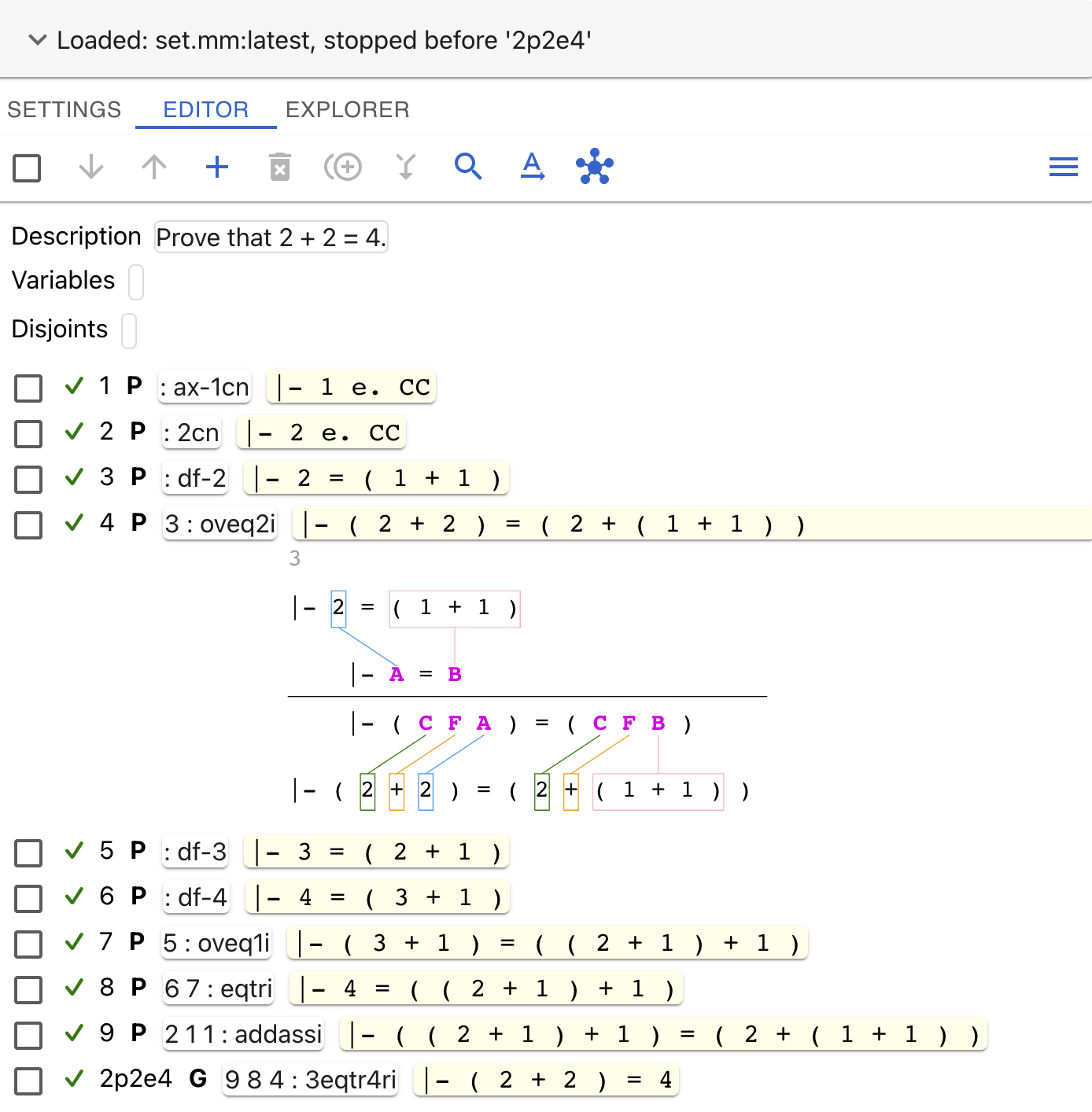
You can start using metamath-lamp immediately by visiting the Metamath-lamp application page, which can import this JSON file proving 2p2e4.

User guide (tutorial)

This is the user guide (tutorial) portion of this overall guide. In this section we will explain how to use metamath-lamp to create some proofs by creating some example proofs. We recommend starting the tool and applying these examples.

We will start with a simple proof that 2 + 2 = 4 (2p2e4), We’ll then follow that with a tour using the Explorer tab, a proof of the principle of the syllogism (syl), and a proof that the reciprocal of the cotangent is tangent (reccot). We’ll close with some other topics, such as a discussion on creating your own examples from existing proofs.

Proof: 2 + 2 = 4

Let’s show how to use metamath-lamp to create a simple proof, namely, that 2 + 2 = 4. This has already been proved in the set.mm database as theorem 2p2e4.

First, we need to start metamath-lamp. Just click here:

Metamath-lamp application page

Selecting the proof context for 2p2e4

We first need to decide on the proof context, that is, the database(s) of axioms and proven theorems we’ll use. In this case we’ll use the most common Metamath database, set.mm. This database uses the very common starting points of classical first-order logic and ZFC set theory. We’ll also tell it to stop using the database just before its proof of 2 + 2 = 4, which in this database is named 2p2e4. If we included the existing proof, the prover would simply reuse that existing proof.

When the tool starts it will say “No Metamath database is loaded, please select a database to load.” Let’s load the set.mm database.

Under “Source type” select “Web”, and under Alias select “set.mm:latest”. After confirmation this will download the selected database. Under “Scope” change “Read all” into “Stop before” enter the label 2p2e4 and select it from the dropdown menu.

We’ll use the term “click” to mean either a quick click with the left mouse button or a quick tap on a touchscreen. A normal click or tap lets you do many things like apply buttons, reveal information, toggle a display, and select some information. We’ll also sometimes say “press” to mean the same thing.

Finally, click on the “Apply Changes” button to accept the selected context.

Adjustments for small displays

Metamath-lamp works really well on small displays like smartphones. However, if you are using a small display, you should consider configuring the tool so it uses less display space.

If you’re using a small display, click the icon menu (menu), and select “View options”. Turn on “Compact mode” and “Small buttons”. Press Close.

We will later cover more tricks for small displays.

Setting the goal statement for 2p2e4

We need to tell metamath-lamp our goal. So we’re going to add a statement and type in our goal statement.

In the Editor click on the icon add (add new statement). Don’t try to click on the similar icon duplicate as that would try to create a duplicate (the tool won’t let you do that anyway). Enter |- ( 2 + 2 ) = 4 and press Enter (Return) to save the result.

After editing, instead of pressing Enter (Return), you could also click on the icon save (save) or the icon cancel (cancel).

Be sure to surround each symbol by at least one space (the first and last symbols can start and end the statement). If you make a mistake, it will show an error; you can then long-click on the statement to edit it.

The set.mm database has strict rules about parentheses. For example, set.mm requires that infix functions like “+” be surrounded by parentheses. This is very easy to understand once you have some experience with Metamath proofs in set.mm, and it eliminates ambiguity. We will explain the rules in more detail later. For now, if you encounter an error while repeating the first example, please re-check if you typed in all the statements exactly as per the example.

Setting the goal label for 2p2e4

Metamath-lamp assumes by default that the first step you add is the final goal. Thus, this step shows a bold G (meaning that this is the goal) and it’s given the goal’s default label qed.

For our purposes, we’re going to rename the label of our goal. Renaming the label of the goal (or any other step) is not required by metamath-lamp. You could instead just continue using the label metamath-lamp suggested. But renaming some of the steps (especially the goal) makes them easier to distinguish for you. Also, the label of the goal will appear in the final generated proof, so it’s best to at least rename the goal.

In general, if you plan to eventually add this proof to the set.mm or iset.mm databases, then you need to follow the set.mm database conventions, including the set.mm label naming conventions. In this case, the conventional name for this goal would be 2p2e4.

But now we need to learn a general rule about the metamath-lamp user interface:

Edits generally require a long-click.

There are multiple ways to do a long-click. Using a mouse, you can press down on the mouse, wait a second, then release. Using a touchscreen, you can press down on the screen, wait a second, then release. With a mouse you can also use a shortcut: hold the Alt key (sometimes labelled Opt or Option instead), then click with the mouse. There are a few shortcuts, and you can use the Settings tab to change some defaults, but for now let’s use the default configuration.

So let’s rename this goal step to 2p2e4:

Long-click on the label of the first step, which is currently named qed. Change the name of the step from qed to 2p2e4 and press Enter (Return).

Setting the description for 2p2e4

It’s not required, but it’s often useful to have a description. Let’s set one.

Long-click on the box to the right of the word “Description”. When it opens for editing, enter the text Prove that 2 + 2 = 4. Press Enter (Return).

Metamath-lamp has many shortcuts. For example, you can also edit fields by clicking on the name of the field (e.g., by clicking on “Description”).

By the way, did you notice something about when we set the description? The quick start said that you can set the description first and later add the goal. You can, of course, do that. Yet in this tutorial we added the goal first and later we added the description, which is in the opposite order. We did that to prove a point.

Final Metamath proofs must adhere to extremely rigorous standards. In particular, every step must be justified by an axiom or proven theorem and can only use previous steps as their (essential) hypotheses.

However, metamath-lamp is flexible in supporting how you reach this rigorous objective. You can generally provide information in whatever order you prefer. In some cases metamath-lamp will warn you that there’s a problem via error messages, but you can then correct the error. You can work backwards from a goal, work forwards from what you know, or even just record what you know that you think might be useful. In some cases it’s more convenient if you do things a certain way. For example, the first step you add will be marked as the goal, so it’s convenient if you describe the goal as your first step. However, this is just a convenience; you can change what the goal is at any time.

Interlude: Brief review of metamath-lamp user interface

Let’s look at the display we have so far (your screen may look somewhat different):

Metamath-lamp display with just the `2p2e4` goal

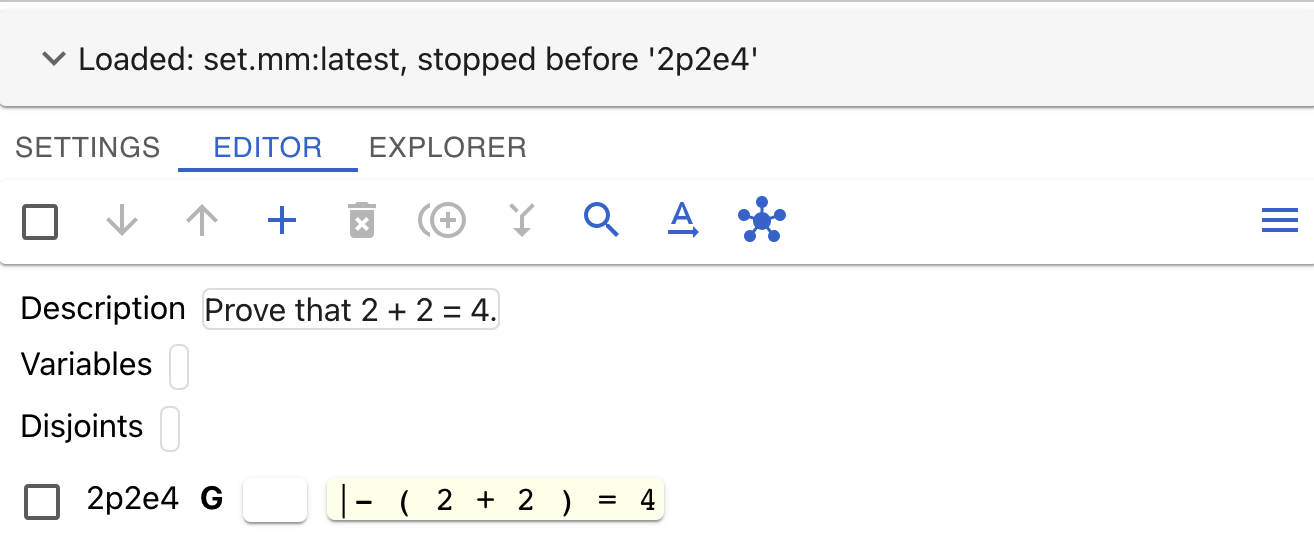
The top line summarizes the context - we loaded the set.mm database (classical logic and ZFC set theory) and stopped reading the database before 2p2e4.

The next line is the tab bar, letting you select between various tabs. These tabs always include Settings, Editor, and Explorer, and may include other tabs too. If you want to change the configuration of the tool, use Settings. You’ll normally be in the Editor tab when editing proofs, so we’ll focus on that.

Below the word “Editor” is the editor command icon bar. The editor command icon bar shows many different icons; each icon represents a command you can use to modify a proof. We’ve already used one icon, the icon add that adds a new statement and looks like a “+”. The reference manual section Editor command icon bar discusses each icon and the command it performs in more detail. You can hover over an icon to see what the command is.

Here’s a list of the icons in the editor command icon bar and the command each icon performs:

Icon	Meaning	Visual Description	Additional information
checkbox	Select all	Checkbox	Select or deselect all current steps
down	Down	Down arrow	Move the selected steps down the list
up	Up	Up arrow	Move the selected steps up the list
add	Add new statement	Plus sign	Type in the new statement
add	Delete selected steps	Trash can
duplicate	Duplicate selected statement	Circles behind “+”	Makes a copy of the selected statement
merge	Merge similar steps	Merge	Select one statement
search	Search	Magnifying glass	Add new steps by searching for a pattern; see search patterns
global substitution	Substitution	A with arrow	Apply a global substitution (aka replacement) to all statements in the proof; see global substitution
Unify	Unify	Hub	Unify all steps or unify selected provable bottom-up. If no steps are selected, attempt to unify everything. If one statement is selected, open proving bottom-up dialogue
menu	Menu	3 horizontal lines aka hamburger	Menu of other actions

Under the editor command icon bar is basic information about the proof (such as its description) and steps for the proof. We see one step already, with the label 2p2e4. Every step has a box on its far left, which lets you select (or deselect) the step to choose what to act on.

Terminology: A proof is a series of one or more steps. A valid proof must have at least one step (the goal). Each step has a collection of information, shown left-to-right:

• Checkbox to show if the step is selected.
• Label (to identify it). A step label is sometimes informally called a step id or step name.
• Step type (a goal G, an (essential) hypothesis H, or another provable statement P). A goal is a special kind of provable statement. (When we say “hypothesis” in this document we mean a Metamath “essential hypothesis” unless we specifically say otherwise.)
• Justification (if any) - the reason the statement is true.
• Statement (a claim, typically beginning with |-).

In a completed proof, each step used in a proof must have a justification (that is, it’s either a hypothesis, or it references an axiom or theorem, possibly using previous steps as its hypotheses).

Now that we’ve had a brief introduction to the metamath-lamp user interface, let’s decide how to use it to create our proof.

Deciding on a proof strategy for 2p2e4

Now we need to figure out how to prove this goal.

Metamath-lamp can do some things automatically. However, we will intentionally avoid some of those automations to see how to prove something in cases where the automations can’t do enough.

There are many different ways to create a proof, including backwards from the goal, forwards toward the goal, or any other order. Metamath-lamp supports them all. Also, note that there are often many different proofs for the same true final statement. Here we’re going to show one way to do it, as an example.

In many cases we can prove a statement by identifying definitions of what we want to prove, finding their expansions, and repeatedly expanding and simplifying the results to show that what we want to prove is correct. Let’s take that approach.

Expanding the definition of 4

In this case, we want to prove that something is 4, so the definition of 4 would probably be useful. We’ll search for the definition of 4 so we can add it to our list of steps.

Click on the icon search (search); under the field name “Pattern” enter 4 = 3 + 1 and click on Search. Metamath-lamp will produce a list of every assertion where the conclusion has the symbol 4, then eventually =, then eventually +, then eventually 1. Select the step labelled df-4 and press “Choose Selected” (you may need to scroll down to get to “Choose Selected”). You will now have a new step with a label of 1 and this statement: |- 4 = ( 3 + 1 )

Notice that in each step, to the right of the label and the left of the statement (starting with |-), there is a bold letter P. This bold letter P is the step type; the P means that this step is intended to be provable. In some cases you’ll want a step to be an (essential) hypothesis (something assumed) instead being provable. You can select the P with a long-click to change it to an H (hypothesis) or back to P (provable). We aren’t going to use any hypotheses in this proof, so we won’t do that for now. The first step we created has the step type G (goal); the goal is a special type of provable statement.

This definition of 4 depends on the definition of 3, so let’s add the definition of 3 as well. Note that df-4 is the definition of 4; this suggests a naming convention, so we can probably just use the naming convention to find it.

Select the icon search (search); in the “label” field enter df-3 and click on Search. Select the step labelled df-3 and press “Choose Selected”. You will now have a new step with a label of 2 and with this statement: |- 3 = ( 2 + 1 )

We can connect the definition of 4 using the definition 3 by simply adding 1 to both sides of the definition of 3. We can simply add a step that claims this statement and see if metamath-lamp can find a justification that proves this is correct (in this case it can). In fact, if each step makes very small changes, metamath-lamp can sometimes prove many statements automatically.

Click on the icon add (add new statement). Enter, for this new step, the statement |- ( 3 + 1 ) = ( ( 2 + 1 ) + 1 ) and press Enter (Return). Now, while no steps are selected, click on the icon Unify (unify). Since there was no specific step selected, it will try to justify all steps.

Metamath-lamp will succeed in finding a justification for our new step, so it will show a green checkmark next to our new step. The justification it will show is 2 : oveq1i, which means that it can justify this new statement by applying theorem oveq1i and providing step 2 as the hypothesis required by oveq1i.

Using statement fragments to connect 3 + 1 with 4

We could later on connect this proof of the meaning of ( 3 + 1 ) to the number 4. However, in a more complex proof we might forget that we were trying to prove an expansion of a value used in the goal (4 in this case). So let’s “clean up” now by directly proving that this term is an expansion of a symbol in the goal. Instead of typing it all in, we’ll use the “duplicate” command to get us started:

Click the checkbox icon checkbox (select step) to the left of the new step 3 (not the checkbox icon checkbox (select all) on the editor command icon bar), Step 3 is the step with |- ( 3 + 1 ) = ( ( 2 + 1 ) + 1 ) as the statement. Click on the icon duplicate (duplicate).

This will create a duplicate step (labelled 4) below the selected step (labelled 3). The tool will also complain that there’s a duplicate. Let’s fix that. We could long-click on the new statement text to edit it, and change its ( 3 + 1 ) to 4. However, this is a good time for us to introduce metamath-lamp’s support for statement fragments.

Click (do not long-click) on the open parenthesis “(“ to the left of “3” in our new (duplicate) step. This will open a statement fragment icon bar below the statement and select ( 3 + 1 ) as a fragment. If you didn’t get the right fragment selected, just try again.

A normal click on a symbol in a statement enables metamath-lamp’s statement fragment mechanism, which lets you select and manipulate fragments of statements in a syntax-aware way. This lets you manipulate text in sensible ways and eliminates tasks like the need to count parentheses.

Exactly what statement fragment is selected depends on the symbol you choose. If you select a parentheses-like symbol, it selects the expression that begins or ends with that symbol. If you select an infix symbol, it selects the expression immediately surrounding the infix symbol. You can then modify the selection, for example, you can use the icon expand (expand selection) and the icon shrink (shrink selection) to expand or shrink the selected sequence of symbols in a syntactically-aware way.

Here is the meaning of each icon in the statement fragment selector:

Icon	Meaning	Visual Description	Additional information
expand	Expand selection	Zoom in	Expand the selection to the next larger syntactic unit
shrink	Shrink selection	Zoom out	Reduce the selection to the next smaller syntactic unit
add above	Add new statement above	Arrow up from box	Create a new step above the current step with the selected statement fragment
add below	Add new statement below	Arrow down from box	Create a new step below the current step with the selected statement fragment
copy	Copy to clipboard		Copy the fragment into the clipboard
edit	Edit	Pencil	Start editing with current text selected
cancel	Cancel	Circled X	Cancel (and close) this statement fragment dialogue

You can use a fragment selector on more than one step at the same time; this is useful, for example, when doing a global substitution.

In this case, we’ll change ( 3 + 1 ) to 4:

Click on the icon edit (edit) in the newly-revealed statement fragment icon bar. This will begin editing the statement with the fragment selected. Type 4 - note that entering text will immediately replace the selected text, in this case ( 3 + 1 ). Now press Enter (Return).

We now have a new step with the statement |- 4 = ( ( 2 + 1 ) + 1 ). Let’s unify to see if the tool can find a proof for this claim.

Click on the icon Unify (unify).

This will produce a green checkmark next to our new step. We have green checkmarks next to all the steps except our final 2p2e4 step.

Expanding the meaning of ( 2 + 2 )

Our goal involves showing that the symbol 2 and 4 have some kind of relationship. A common technique to create proofs is to expand the definitions of terms and then show that their expansions are equivalent. We’ve already expanded 4, let’s now expand 2.

Select the icon search (search). In the “label” field enter df-2 and click on Search. Select the step labelled df-2 and press “Choose Selected”. You will now have a new step with this statement: |- 2 = ( 1 + 1 )

This definition of 2 is similar to the value we expanded for 4. Both have a 1 followed by another 1 at their end. We can take the definition of 2 and add 2 to both sides, at the beginning of each side, to produce a very similar expression. Let’s try that.

Click on the checkbox icon checkbox (select step) to the left of the new statement |- 2 = ( 1 + 1 ) to select that step, then press the icon duplicate (duplicate). Use long-click on the new statement and modify it so that it is |- ( 2 + 2 ) = ( 2 + ( 1 + 1 ) ) and press Enter (Return).

While editing this statement you may find some parentheses appear automatically in unwanted places. This is intended to be a handy feature when writing new statements, but sometimes when editing it doesn’t help. Please remove unwanted parentheses and make sure the statement looks exactly as in the example.

Feel free to use statement fragment selectors instead to make this change.

Now click on the icon Unify (unify), Since there was no specific step selected, it will try to justify all steps.

Metamath-lamp will succeed in finding a justification for our new step, so it will show a green checkmark next to our new statement and its justification (5 : oveq2i in this case).

Showing these expansions are equal

At this point we’ve shown that 4 and ( 2 + 2 ) are separately equal to very similar expressions. If we could prove that those expressions are equal to each other, we could trivially prove our goal. Let’s try to do that.

Click on the checkbox icon checkbox (select step) of the 2p2e4 goal step. Click on the icon add (add new statement).

We’re duplicating a goal step. The tool knows there’s only one goal, so in the duplicate the step type will be turned into a provable (P) step type. By default the goal is kept at the end, so this new statement will be added just before the goal step.

Now let’s edit the new statement.

It’s usually best, when creating Metamath proofs, to try to minimize the differences in statements between each step, such as swapping the left-hand-side and right-hand-side of an equality. There are other tools that can help you minimize the number of steps in a Metamath proof, once you have a valid proof.

So what I would typically do, if I was just entering this by hand, is replace the ( 2 + 2 ) with its equivalent ( 2 + ( 1 + 1 ) ), and replace 4 with its equivalent ( ( 2 + 1 ) + 1 ). That would lead to this final statement:

( 2 + ( 1 + 1 ) ) = ( ( 2 + 1 ) + 1 )

As humans we know this is true. That’s because addition is what’s called associative, that is, when two additions occur in a row, you can start with either the first or second addition and the result will be the same.

Does the Metamath database in our current context have this information? Well, I’ve previously searched for the rule in set.mm proving that the addition of complex numbers is associative, and it does have a proof the addition is associative. However, in the database the left and right hand sides are swapped. Normally, if I knew that fact, I then add an additional step above this one with the left and right sides swapped to match the database. If you provide many intermediate steps, metamath-lamp can often complete the proof more quickly.

However, for demonstration purposes, I’m going to swap the two sides ahead of time. I want to show that sometimes simple unification doesn’t work, even when you know you’re matching a theorem’s pattern exactly. I also want to show that while it can be helpful to take small steps, it isn’t always needed (that is, both the expanded goal and the version that matches the database pattern). But first, let’s try out this sequence that addition is associative, and see that simple unification doesn’t work:

Long-click on the statement of the new step. We’re going to add as our new statement the required equivalence, but with the left and right hands of the equality the same as set.mm (and thus swapped compared to the goal). Enter |- ( ( 2 + 1 ) + 1 ) = ( 2 + ( 1 + 1 ) ) and press Enter (Return). As an experiment, select the icon Unify (unify) while there’s no step selected; you’ll see that in this case it did not find a justification for our new step.

Yes, it’s true that ( ( 2 + 1 ) + 1 ) is equal to ( 2 + ( 1 + 1 ) ), the Metamath database in this context already has a proof that addition is associative using this specific order.

However, when you click on the icon Unify (unify) without selecting any steps, metamath-lamp will not automatically prove this new step. As I mentioned a moment ago, I intentionally ordered the statement to match the form in the database exactly - so why isn’t metamath-lamp finding this match and verifying it?

This isn’t unusual. It often happens that we can’t just directly use a rule in the database, but instead we must first prove some other statements before we can use a rule in the database. Sometimes we have to do this for several layers. Metamath-lamp has a tool called “bottom-up search” that will let us find such proofs; it can even find proofs with deeper depths. Before we use bottom-up search, let’s explain what’s going on in detail in this case, as an example of this kind of problem.

This Metamath database does already have the fact that addition is associative. In fact, it has the rule in exactly this order of symbols - I specifically rigged it that way. So why can’t our simple unification work? The problem is that the rule in set.mm requires other information. In this case, the rule that addition is associative requires us to show, as hypotheses, that the values being added are complex numbers. None of our current steps prove that 1 and 2 are complex numbers. The database also has those facts, but they need to be brought in as their own steps before they can be used in this proof.

There’s no need for you to have known this ahead of time. I’m simply trying to illustrate a general point: sometimes theorems require other information to be proved first, even if what you want to prove precisely matches a conclusion in the database.

So we’ll instead use a bottom-up search, which will try to find and prove any other steps necessary to prove a step. A bottom-up search can add new steps, and it can also find multi-step-deep proofs. The search will then return various options, preferring options that have the fewest unknowns left to prove (ideally none of course). You enable a bottom-up search by selecting the single step to be proved and then clicking on the icon Unify (unify).

Click on the checkbox icon checkbox (select step) of the 2p2e4 goal step. |- ( ( 2 + 1 ) + 1 ) = ( 2 + ( 1 + 1 ) ) and click on the icon Unify (unify). A new dialogue will display titled “Proving bottom-up”.

This will enable us to search for a solution backwards from our currently-selected step using the context and previous steps that will help us prove the selected step. These dialogue options control how metamath-lamp will search for a proof of the selected step’s statement.

When you adjust the parameters you are generally making trade-offs; allowing the search to do more will increase the likelihood of finding a proof, but will also make the search time take longer. Experience will help you learn how to adjust these parameters to find proofs with minimal time. For now, we’ll turn off “Allow new disjoints” and turn off “Allow new variables”, because I doubt they will help, but I will make sure I leave on “Allow new steps” because I expect I will need to add new steps. Let’s let metamath-lamp try to prove this!

Press the “Prove” button at the bottom of the dialogue.

After a moment it will present a list, and one of the first options (probably the first one) should use addassi. The theorem addassi is a pre-existing theorem showing that addition is associative. This requires multiple lines, because using this associativity theorem requires showing that 1 and 2 are complex numbers.

Use the checkbox to its left to select that one, then press the “Apply Selected” button.

Suddenly a lot has happened. We now have new steps that have been automatically added to our proof, namely that 1 e. CC (1 is a member of the set of complex numbers) and 2 e. CC (2 is a member of the set of complex numbers).

We have successfully proved that 2 + 2 = 4

We now have a green checkmark next to all our steps, showing that all steps have been proven.

Most importantly, the final step 2p2e4 now has a green checkmark, which means we have proven our goal! Metamath-lamp automatically unified all the steps, and was able to complete the rest of the proof given what we had provided.

If you are new to Metamath and not familiar with formal systems, you may probably not understand how the program knows when to mark a step with a green checkmark meaning it is proved. The short answer is that the green checkmark means that metamath-lamp is able to find, for that step, a specific theorem or axiom that justifies the claim (as well as recursively all of its justifications), possibly using steps previous to that step.

Renumbering steps

Let’s briefly clean things up. The step labels are mostly arbitrary, but it’s sometimes convenient to have them in order. Let’s renumber the numbered steps.

Click the icon menu (menu), and select “Renumber steps”.

The menu shows many less-used commands. This specific command will renumber the step labels that are non-negative integers Step labels don’t need to be non-negative integers (e.g., 2p2e4); those steps will keep their labels as-is.

Getting the completed proof

We can now show the compressed proof. This is the final proof we can add to a Metamath database.

Select the goal step by clicking on the checkbox icon checkbox (select step) to the left of the goal step. Click on the icon menu (menu), and select “Show completed proof”.

This shows the compressed proof. You can use checkboxes to also show the proof table. If you show the proof table, you can also decide if you want it to include the proof of the syntax (type) claims as well as the essential steps.

You can select “Copy” to copy the compressed proof into the clipboard. Press “Close” to dismiss the dialogue box.

Exporting and importing your current state

You can only generate a final proof once you have a proof.

Metamath-lamp can export the current state of your efforts, whatever they are, and anyone can reload them later. This lets you share your current state, even if that isn’t complete.

Click on the icon menu (menu) on the top right of the display.

You can save your state for reloading later in a JSON format:

• “Export to JSON”: Provides the current proof assistant state as text; you can save this where you wish.
• “Import from JSON”: Allows you to load a state previously exported with “Export to JSON”.

If you store this information in a file they conventionally have a .lamp.json suffix (e.g., here’s our JSON file proving 2p2e4).

You can click again on the icon menu (menu) to dismiss the menu.

Looking at proof steps

Let’s look at the proof steps in more detail to gain a better understanding.

In Metamath, every step of a valid completed proof must be an application of an axiom, proven theorem, or previously-proven step. Metamath-lamp shows when it can verify this for a step (after unification) by displaying a green checkmark. It will also fill in the “justification” text.

For example, let’s look at what is now step 4, |- ( 2 + 2 ) = ( 2 + ( 1 + 1 ) ):

Near this step you’ll see a number, a colon, and oveq2i. This means that this particular step is justified (proven) by using the already accepted theorem oveq2i when applied to that labelled step. Advanced users can edit this (with a long-click) to force metamath-lamp to try to use a different justification. While editing you can click on the icon delete (delete) next to the justification to delete entirely, e.g., because you want to prove it some other way.

But what does this justification mean? Visualizations can help, so let’s discuss them.

Visualization: a powerful metamath-lamp capability

Metamath-lamp can provide visualizations to show you what a given justification means for a given step. This only works when the tool has verified the justification and thus shows a green check (or orange “~”). So let’s first use unify to ensure that we’ve proven what we want to visualize.

While no step is selected, click on the icon Unify (unify).

All steps have green checkmarks, which means all steps are proven. Let’s visualize a step:

Click on the green checkmark or the step label for the step showing oveq2i (this is probably step 4). Remember, this needs to be a short click, not a long click.

You should see a visualization like this:

Visualization of (2+2)=(2+(1+1))

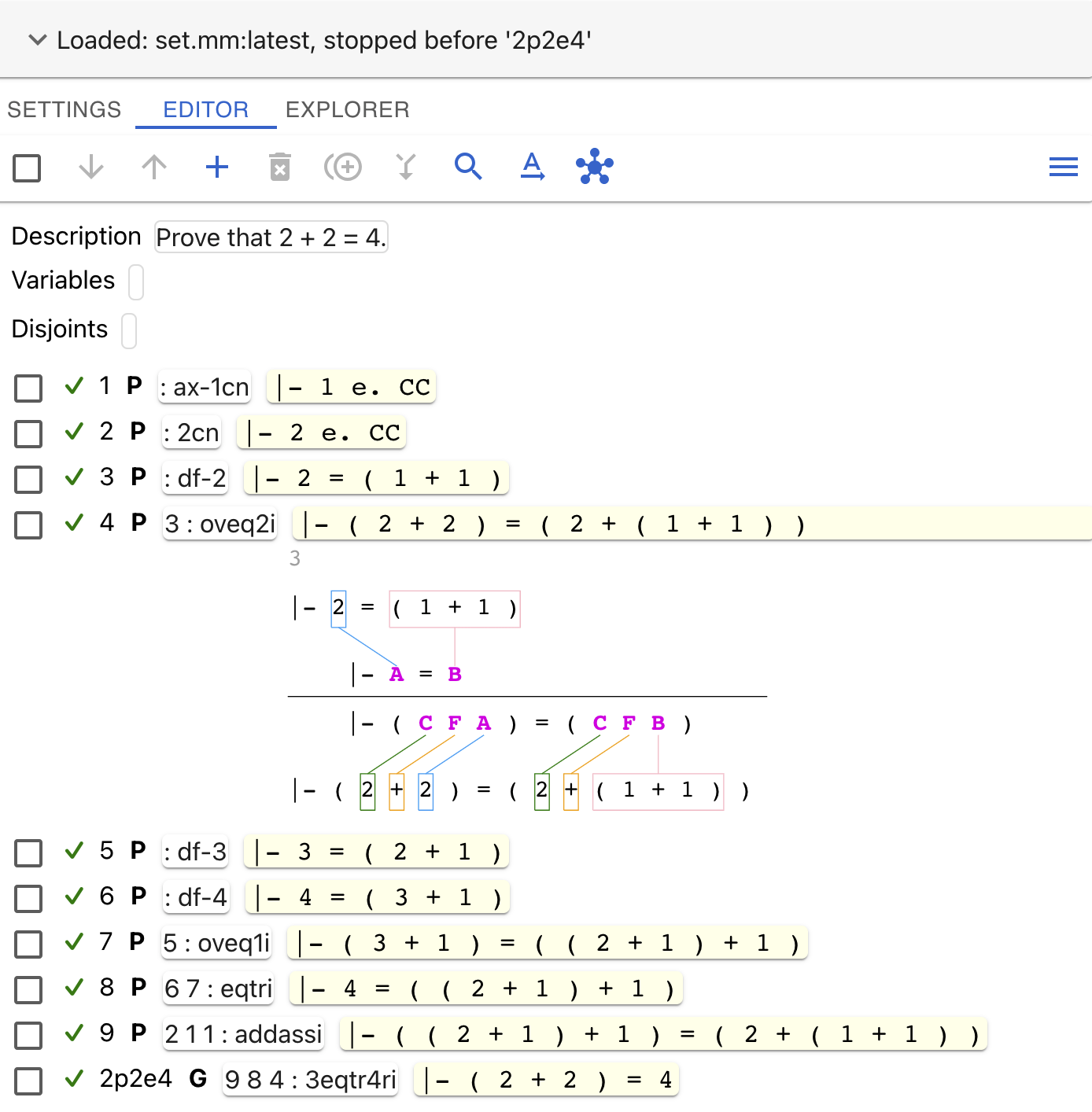
The top new line is the sequence of labels being used as inputs into the justification. In this case there’s only one label; the label you see may be different than what’s shown here. Under that is a copy of each statement from each label, which in this case is one statement:

|- 2 = ( 1 + 1 )

Notice that variable parts of this statement are boxed and directed lines connect them to another statement below.

In the vertical center of a visualization is always a sequence with zero or more statements from left to right (the hypotheses of the reference being used), below that is a a horizontal line, and below that is the reference’s concluding statement. This is a common mathematical representation of a rule &em; a horizontal line with the preconditions above and the postcondition below. In this case we’re using the reference oveq2i as the rule, which requires some statement of the form |- A = B and can then produce |- ( C F A ) = ( C F B ).

The small connecting boxes and lines show that in this use of oveq2i, A will be 2, and B will be ( 1 + 1 ).

The results of oveq2i are always in the form |- ( C F A ) = ( C F B ). Any variable in its output must have the same values as this application of its inputs; C and F have no inputs, so they can be anything syntactically valid. This means we can use oveq2i to justify the final claim, |- ( 2 + 2 ) = ( 2 + ( 1 + 1 ) ).

We can also hide the visualization any time.

Click on the green checkmark or step label for |- ( 2 + 2 ) = ( 2 + ( 1 + 1 ) ) to toggle the display of its visualization; since it is currently displayed, this will hide it.

Let’s try out visualization on the statement that uses associativity, |- ( ( 2 + 1 ) + 1 ) = ( 2 + ( 1 + 1 ) ),

Click on the green checkmark or the label for |- ( 2 + 2 ) = ( 2 + ( 1 + 1 ) ) to toggle the display of its visualization. Since it’s not currently revealed, it will be revealed.

Let’s end its display.

Click on the green checkmark or step label for |- ( 2 + 2 ) = ( 2 + ( 1 + 1 ) ) to toggle the display of its visualization, hiding it again.

Please do try out visualization of different steps.

We think seeing several visualizations will help you better understand how it all works.

Changing the order of steps

You can change the order of the steps (as opposed to renumbering them). Sometimes you need to reorder steps, because steps can only be justified by the context (axioms and proven theorems) and previous steps. A justification can’t refer to a later step, since that would allow circular reasoning.

To reorder some steps, just select one or more using the checkboxes on the left. You may then use the icon up (up) to move them up, or the icon down (down) to move them down.

Click on the checkbox next to |- ( 3 + 1 ) = ( ( 2 + 1 ) + 1 ) and then click the icon up (up) - the step will move up. Click on the icon down (down) to move it back.

Metamath-lamp will display an error message if a justification depends on some other step that does not precede that justification.

Another (easier) way

Metamath-lamp’s bottom-prover could have automated more for us when creating this proof.

Let’s return to our earlier situation before we added statements that used the fact that addition is associative. Here’s how we could do that:

Use the checkboxes to select the steps with the statements 1 e. CC, 2. CC, and |- ( ( 2 + 1 ) + 1 ) = ( 2 + ( 1 + 1 ) ). Click on the icon delete (delete) to delete those steps. Now long-click on the justification for the goal, and select the icon delete (delete) below it to delete its justification.

We’re now in the state we were in before we added the assertion that addition is associative.

We didn’t have to hunt for the theorem that addition is associative. We could have let metamath-lamp do more for automatically.

Here’s one way. We could have selected the goal, and clicked on the icon Unify (unify) to start a bottom-up search directly on the goal.

We will now want to set up the search options to find the proof automatically.

just like before, enable “Allow new steps” and disable both “Allow new disjoints” and “Allow new variables” (because I don’t expect the latter to be helpful in this case). Change the “Statement length restriction” to “Unrestricted”, while leaving the search depth at 4. Now click on the allowed statements both at the “first level” and “other levels”, and enable only the statements I expect to use, which are ( 2 + 2 ) = ( 2 + ( 1 + 1 ) ) and 4 = ( ( 2 + 1 ) + 1 ). Click on “Prove”.

Here are some tips about bottom-up searches. I find it helpful to choose several search options, starting with ones that will run quickly but are less likely to automatically find a proof, If those quick approaches don’t work, then I’ll expand the search parameters so they’ll take longer but will be more likely to be successful. Of course, repeatedly using the tool will give you a better sense of what is more (or less) likely to work.

On my computer it takes 12 seconds to automatically find some proofs using associativity. Notice that you didn’t need to tell it about associativity; given the right search criteria, the tool could find these steps all by itself.

A brief discussions on settings

The Settings tab lets you change various configuration options.

You must press on “Apply Changes” for changes to be applied. Any changes you make in the Settings tab are not applied until you select “Apply Changes”. If you want to discard changes, select “Discard Changes”.

One setting in particular that you might want to change involves how to interpret left click. Should you edit statements with a click or a long-click? The choice is yours. By default, editing statements uses a long-click.

More tricks for small displays

Metamath-lamp works well on small displays, such as the built-in display of smartphones. We already suggested a few adjustments for small displays.

If you’re still cramped for display space, there are some more configuration tricks you can use:

• You can click on the icon menu (menu) and select “View options”. Then disable or enable whatever you’d like. On a small display you probably want to at least enable “Compact mode” and “Small buttons”. You might want to disable display of information you don’t need, for example, you might disable displaying the label or justification. You can always redisplay them later the same way.
• If you disable display of the justification, you can still reveal the justification and/or visualization for any specific step. Just click on the green checkmark, label, or step type (not a long-click) to reveal or hide the justification text. Once revealed, you again click on the icon delete (delete) to delete this justification. You can also click on the icon hide justification (hide justification) to hide the justification, or click on the icon visualization (show/hide visualization) to show or hide the visualization.
• You can click on the icon menu (menu) and select “Hide tabs”. This will stop displaying the tab bar; to see it again, click on the icon menu (menu) and select “Show tabs”.
• Click on “Settings” in the tab bar and click on “hide context header”. Be sure to “Apply Changes”. If you want to change the context, you can change the settings. You might find it easier, from the editor, to just click on the icon menu (menu) and select “Show context” when you want to see the context; collapsing the context will hide it again.
• In your web browser change the font size (e.g., to something smaller). In Chrome, use Settings / Accessibility and adjust the text scaling. In Firefox, use Settings / Accessibility, disable automatic font sizing, and adjust the font size.

A tour using the Explorer tab

The tab bar lets you switch between tabs, and those tabs always include Settings, Editor, and Explorer. The Explorer tab lets us view the assertions (axioms and theorems) in the current loaded context.

Of course, if you want to see the “final” rendering of a widely-used Metamath database, you can easily go to the Metamath Home Page. On that website you can see nicely rendered versions of the Metamath Proof Explorer (set.mm), Intuitionistic Logic Explorer (iset.mm), New Foundations Explorer (nf.mm), and the Higher-Order Logic (HOL) Explorer (hol.mm). Those web pages have many advantages. Each assertion has its own URL, loads quickly, and displays well even when JavaScript is disabled on the web browser. The Metamath home page renderings have been generated in a “pretty” format and include a lot of information about each assertion (such as syntax hints for every symbol used, the axioms and definitions it transitively uses, and what assertions reference it). It groups the axioms and theorems into chapters and further subsections, with descriptions of each section. Finally, those sites come with additional pages of documentation that explain various important features.

However, the built-in metamath-lamp explorer has its own advantages. The metamath-lamp explorer will always show you the current context. This means, for example, you can explore other databases (such as a database on local storage or a historical database), as well as portions and combinations of databases. The metamath-lamp explorer also includes its fragment selector (so you can copy fragments found from exploration) and visualization mechanism (to help you better understand the database). You can also use the metamath-lamp explorer to explore databases while disconnected from the internet. In short, the explorer tab lets us see the context we’re using.

But before we dive in, let’s admire the magic.

Warning: Magic here

Truth is precious, because truth is hard to find and harder to confirm. One of the beautiful things about mathematics is its potential to achieve an eternal kind of truth. Once something is correctly proven it will always be true (for the assumptions of that proof). Sadly, this beauty is sometimes hidden.

Magic Hat image

Metamath is in some ways a kind of magic, because with Metamath you can view the full chain of logic from high-level proven ideas all the way back down to axioms, with no exceptions. There is magic in showing that geometry, algebra, calculus, topology, and many other mathematical domains can all be built from a few very simple axioms. But this is not the kind of magic that creates mystery - it's the kind of magic that reveals mysteries.

The metamath-lamp explorer, and the explorers on the Metamath Home Page, all let you discover these truths, including their web of surprising interconnections. In this section we’ll learn how to use the explorer in metamath-lamp.

Loading a context for the explorer

You need to have a context loaded before the explorer tab is useful. For our purposes we’ll use the set.mm database. If you’re continuing the tutorial, you’ve already done that.

However, if you’re starting at this point, first load set.mm as the context:

Make sure we are loading from the web the file “set.mm:latest”, You can change the scope stopping before 2p2e4 or just load the whole database, your choice. Then press “Apply changes” to apply this change.

Trying out the explorer tab

Let’s try out the explorer tab:

Click on “Explorer” in the tab bar.

The explorer view lets you see the various assertions (axioms and theorems) in the current context.

The top of the explorer view lets you select what to view; by default all assertions are included. There are typically many assertions, so this is a paged view.

Below the selection options is a list of assertions (theorems and axioms). Each assertion shows its numeric position, the type of assertion (theorem or axiom), and the assertion label in bold. The rest of the display shows a list of 0 or more hypotheses, each prefixed with large black circle “⬤”. The final line of an assertion states what can be concluded via this assertion when its hypotheses are true.

The order of assertions is important. In particular, a theorem can only refer to previous assertions; this eliminates the possibility of circular reasoning. Also, when you tell metamath-lamp to limit the scope to either before or after some assertion, your proof can no longer refer to any assertion after that (until you change the context’s scope).

Let’s look at axiom ax-mp, which is probably assertion number 5 in your display. Axiom ax-mp is called modus ponens and is well-known.

Scroll down (if necessary) to see Axiom ax-mp.

Here is what axiom ax-mp (modus ponens) looks like in the explorer display:

Axiom ax-5 (modus ponens) in the explorer tab

Axiom ax-mp (Modus ponens) has two (essential) hypotheses:

• |- ph - that is, “when ph is true”, and
• |- ( ph -> ps ) - that is, “when ph implies ps”

Using axiom ax-mp, whenever those two hypotheses are true, you can prove “ps is true”. Note that ph and ps are variables over any well-formed formula (wff) expression, that is, anything that is true or false; they are not limited to being replaced by just another variable. The axiom modus ponens can apply to many circumstances.

From the explorer you can use various capabilities. You can use the fragment selector to copy useful portions of any statement. Next to the name of each axiom or theorem is a “>” symbol which lets you expand or hide its description. Let’s try that out on axiom ax-mp.

Click on the “>” symbol to the right of ax-mp (don’t click on the name ax-mp, we’ll try that out later). Notice that this reveals a description; click on the modified symbol “∨” to the right of ax-mp to to hide the description again. Click on the open parentheses “(“ in the second hypothesis of ax-mp; you’ll see that the fragment selector bar has emerged and the expression ( ph -> ps ) has been selected. Click on the icon unselect (unselect) to close it.

A few set.mm symbols

Proof statements’ symbols use ASCII characters. Here are a few symbols and their meanings:

• -> represents “implies”. The left-hand-side of an implication is called the antecedent; the right-hand-side of an implication is called the consequent.
• ph, ps, ch, etc. represent the Greek letters φ, ψ, and χ. These are variables that represent an arbitrary expression with a value of either true or false.
• -. means logical not; if what follows is true then the result is false, if what follows is false then the result is true.

See common set.mm symbols for more.

Viewing proof of mp2

If you click on the label (aka name) of a theorem, you’ll be able to learn more about that theorem.

In explorer, expand a label to show its proof

Let’s try that out now.

In the explorer view, scroll down to theorem mp2. Click on the name mp2 (not the “>” next to it).

Clicking on the name of an axiom or theorem will switch the view to a dynamic tab of that name (creating it if necessary) that shows details about it. These dynamic tables are called individual assertion tabs. The tab bar shows all the currently-opened individual assertion tabs (you can select the “x” next to the tab name to close an individual assertion tab).

In this case, our individual assertion tab is showing us the proof of mp2.

Each individual assertion table begins with a summary of what it is, including a brief natural language description, a list of its hypotheses (if any), and its conclusion.

Below that is a table that shows the steps of its proof. Steps are numbered (starting from one). In each step is a “hyp” (the space-separated list of steps used to justify this step) and a reference to the axiom or theorem used to justify this step. This is followed by the statement proved by this step. From this table:

• Clicking on a hypothesis step label will move the display to that step (this is helpful in long proofs).
• Clicking on a reference to an assertion (axiom or theorem) will switch tabs to that assertion (creating a tab if necessary).
• Clicking on any part of a statement will start the fragment selector there.

At the beginning of each statement (other than the hypotheses) is the icon ⊞ (expand). When a visualization is visible the icon changes into the icon ⊟ (collapse) which, if clicked, will contract the expansion. These visualizations can make it easier to understand how Metamath proofs work.

Let’s try out a visualization in mp2.

Click on the icon ⊞ (expand) next to the statement of step 4.

You should now see a visualization of step 4:

Theorem mp2 with a visualization of step 4

Step 4 is justified by ax-mp (modus ponens). At the center of the visualization is the usual representation of rule: a horizontal line with the preconditions above the result below. Modus ponens has two preconditions: some ph must be true (whatever ph is), and some ( ph -> ps ) must be true (that is, ph implies ps whatever ph and ps are). If these preconditions are met, then per modus ponens, ps is true.

The visualization then shows how the symbols flow in and out of the rule. In this use of modus ponens, we’ll substitute ph with ph (from step 2), and ps will be replaced with ( ps -> ch ) (from step 3). Given those substitutions, the result of this particular application of ax-mp in step 4 is ( ps -> ch ).

Revealing types in the individual assertion tabs

Metamath proofs include proofs of the type of every expression, to ensure that all expressions have valid types. Ensuring that the types are correct is critical to ensuring that the proofs are correct. Metamath verifies types the way it does everything else - there must be axioms that describe valid types, and it must then prove that the expressions being used match the required types.

Normally you never need to see or deal with types. Metamath-lamp will automatically handle type checking for you, and by default the proofs that the types are correct are not shown. However, we think it’s helpful to understand types and what the tools are doing for you. Metamath-lamp can reveal this more detailed view about types if you wish to see this information.

If you click on “show types” just above a proof table, the proof display will include the “syntax” (aka “types” or “inessential”) proof steps. These are steps in a Metamath proof that prove that each expression has a valid type.

Staying in the mp2 individual assertion tab:

Click on “Show types”.

You’ll now see far more steps, which reveal how Metamath proves that every expression is syntactically legal. Step 5 uses reference wps to prove that the symbol ps is a wff (well-formed formula), and step 6 uses reference wch to prove that ch is a wff. Step 7 then proves that ( ps -> ch ) is a wff, referring to steps 5 and 6 and a reference called wi. We can click on the icon ⊞ (expand) in step 7 to visualize what’s going on. This reference wi asserts that if some ph and some ps are wffs, then its corresponding ( ps -> ps ) must also be a wff. In this step, we substitute ps and ch, producing ( ps -> ch ).

This reveals how Metamath ensures every expression has the correct type in an existing proof.

Revealing more about Metamath types in the editor

You can also make the editor reveal whether or not an expression is of a given type. Simply create a step (e.g., via duplication) and change the first symbol (which is typically |-) into a typecode (for set.mm the typecodes are wff, class, or setvar). When you ask it to unify, it will show a green checkmark if it was able to verify that claim.

Let’s go back to the editor and look at our proof that ( 2 + 2 ) = 4 (if you’ve lost that, you can use “import from JSON” to load our proof of 2p2e4 in JSON format.

Click on the checkbox next to step 7 which uses oveq1i. Click on the icon duplicate (duplicate selected statement). In this new step, long-click on the statement, then edit the statement to replace |- with wff. Click on the icon Unify (unify).

You’ll see that this new step is proven, but the justification is different. What we are now doing is proving that a given expression is a wff, that is it’s syntactically legal expression that is true or false. The tool was able to determine that the expression ( 3 + 1 ) = ( ( 2 + 1 ) + 1 ) was true or false, and it justified that using the reference wceq.

We can visualize this step:

Click on the green checkmark on the new step to reveal its visualization.

Editor visualization of expression with ( 3 + 1 )

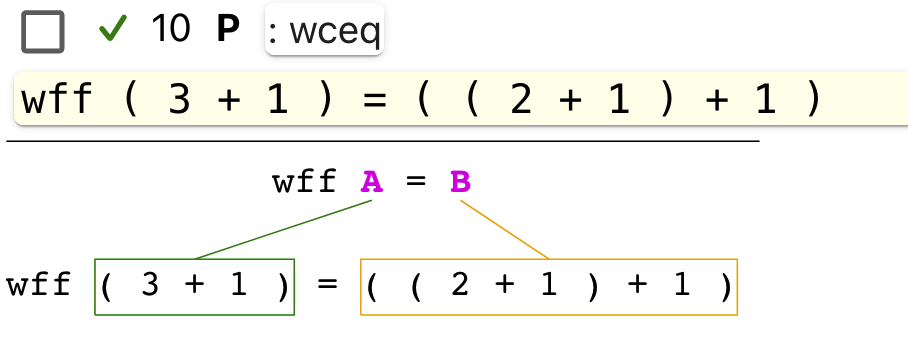
What we’re seeing is that we can justify that an expression is a wff by using the reference wceq. This reference requires the form A = B. In this case, we can see that A can be substituted with ( 3 + 1 ) while B can be substituted with ( ( 2 + 1 ) + 1 ).

We could use the fragment selector to repeatedly copy portions and visualize each one. The ability to select parts to create a new statement (above or below) could be useful. If you wanted something to show others, you could do this. However, that would be tedious to do for a quick view. There’s a simpler solution: use the “bottom-up” prover with a logging level of 1 (to visualize intermediate steps). Let’s try that.

Click on the checkbox of the new statement (1) which uses oveq1i. Click on the icon Unify (unify). To let us interactively expand it, select “logging level 1”. Press “Prove” and then press “Show proof tree”. It will show the justification for the final expression. Repeatedly press the icon ⊞ (expand) to expand the visualization. Once you press the icon ⊞ (expand) it will become the icon ⊟ (collapse) which, if clicked, will contract the expansion.

As you expand, you’ll see a tree emerge. Here’s a view at one point:

Typecode tree of ( 3 + 1 ) = ( ( 2 + 1 ) + 1 )

Here’s an explanation of what these topmost parts of the tree mean (they can be further expanded):

• Step 10: Typecode wff applies to ( 3 + 1 ) = ( ( 2 + 1 ) + 1 )
  • Reference wceq justifies this claim, referring to steps 6 and 1.
    • Step 6: Typecode class applies to ( 3 + 1 )
      • Reference co justifies this claim, referring to steps 7, 3, and 2.
    • Step 1: Typecode class applies to ( ( 2 + 1 ) + 1 )
      • Reference co justifies this claim, referring to steps 4, 3, and 2.

Click on “Close” and “Cancel” to end.

A Metamath proof proves that expressions are of certain types the same way it proves that claims are true. Metamath requires that there be an existing rule (a reference) that can use certain hypotheses as steps to justify a claim, going back to first principles.

Again, normally you do not need to look at type information. This is normally done automatically for you. But we think it’s helpful to understand what the tool is doing “under the hood” with types to ensure that your proofs are correct.

Gaining an understanding of set.mm’s beginnings

You can use the explorer to gain many insights into a database (and mathematics in general). In this section we’ll walk through the first few assertions of set.mm to gain some understanding of this database. (By assertions here we means “axioms and theorems”.)

If you’re already familiar with set.mm, you can skip this section.

Let’s go back to the explorer tab:

Click on the “Explorer” text in the tab bar, and scroll to the top.

Assertion 1: Theorem idi

Let’s gain a brief understanding of the first theorems and axioms. We are entering the foundations of the foundations - the very basement - of the “typical” mathematics of classical logic and ZFC set theory.

Assertion 1 is the theorem idi. In the explorer it looks like this:

Representation of assertion 1, idi

In idi all the statements begin with |- meaning “this is true”. Theorem idi says the following: if we assume that some statement ph is true, then we can conclude that this statement ph is true. Let’s see its description.

Click on the symbol “>” to the right of the name idi.

Every axiom or theorem in set.mm has a description. In this example, you can see that theorem idi was contributed by Alan Sare. The names of people who formalized and proposed various statements are recorded for all time in these descriptions.

☞ We hope to see your name in future database descriptions!! ☜

Theorem idi and the next one a2ii are very peculiar, because they are theorems that can be proven in Metamath without axioms. Metamath verifiers work by using the hypotheses and applying the justifications they are given to show that they can produce what is to be proved. In this odd case, the hypothesis is what needs to be proved, so a metamath verifier is allowed to just use it. Both proofs have 0 essential steps and 1 if you include syntax proof steps (showing that the inputs and outputs match). This doesn’t hurt Metamath’s generality; it’s hard to imagine a useful mathematical system where you’re not allowed to conclude something you assume.

Theorem idi doesn’t let us conclude anything new, so it’s normally not useful. It’s only useful in special technical situations. Notice that the description of idi has a special phrase: “(New usage is discouraged.)”. This phrase tells people and tools that they should not use this assertion in most circumstances. It is true, so you can use it if you want to, and there are special technical situations where it is useful. Currently metamath-lamp doesn’t exclude discouraged theorems and axioms from its automation, but we expect it will exclude them by default in the future.

Assertion 2: Theorem a1ii

Assertion 2 is the theorem is a1ii. It has two hypotheses and one conclusion. All the statements begin with |- which again means “this is true”. Theorem a1ii can be interpreted as saying that if we assume some ph is true, and we assume some ps is true, then we can conclude that ph is true. This simply lets us restate one of two accepted truths. Again, this is only useful in special technical situations, but it’s hard to argue with the conclusion. This theorem is also discouraged.

Assertion 3: Syntax axiom wn

Assertion 3 is wn. This is our first axiom, but it’s not an assertion of truth (|-), it’s an assertion that a certain pattern is a well-formed formula (wff). In short, it’s a “syntax axiom” - a way of asserting that a specific pattern is valid syntax. This assertion says wff -. ph, that is, if some ph is a wff (an expression that is true or false), then -. ph is also a wff. The sequence -. represents “logical not”, and this axiom allows us to use the sequence -. ph as a wff. In short, this axiom permits us to use “not ph” as a syntactically legal expression.

Assertion 4: Syntax axiom wi

Assertion 4 is a similar axiom, stating that ( ph -> ps ) is a well-formed formula (wff) when ph and ps are wffs. Notice the parentheses; since they are specified as part of the axiom allowing the use of ->, the parentheses are required when using -> in the set.mm database.

Assertion 5: Axiom ax-mp (modus ponens)

Assertion 5 is axiom ax-mp, aka modus ponens. This axiom says that if ph is true, and that ph implies ps, then ps is true (whatever ph and ps are). We’ve seen this one before.

Assertion 6: Axiom ax-1

The next 3 axioms define the axioms of propositional logic, that is, the fundamental rules for determining if something is true or false given other values that are true or false. These are the same as, for example, those of Margaris.

Axiom ax-1 is also called “Simp” or the “principle of simplification”. It asserts that |- ( ph -> ( ps -> ph ) ).

If you open the description you’ll see that this formalization was contributed by “NM”. “NM” stands for Norman Megill, the original creator of the Metamath system. Once again, this shows that we give credit to those who take the time to formalize mathematics.

Again, we hope that you’ll create Metamath proofs and get credit too!

Assertion 7: Axiom ax-2

Axiom ax-2 is also called “Frege”. It asserts that |- ( ( ph -> ( ps -> ch ) ) -> ( ( ph -> ps ) -> ( ph -> ch ) ) ) This looks more complex than it is; it really just “distributes” an antecedent over two consequents.

Remember to open the description using “>” if you are interested.

Assertion 8: Axiom ax-3

Axiom ax-3 is also called “Transp”. It asserts that |- ( ( -. ph -> -. ps ) -> ( ps -> ph ) ).

Assertion 9: Theorem mp2

Theorem mp2 is our first useful theorem (that is, a claim proven using axioms and/or theorems). This theorem proves a claim that involves applying modus ponens twice.

Going beyond

There are many more theorems, of course. We should briefly point out one, syl. The theorem syl proves that if ( ph -> ps ) and ( ps -> ch ), then ( ph -> ch ). This is one of the most commonly-used theorems in the entire set.mm database.

These are very basic beginnings. What’s extraordinary is that you can build up, assertion by assertion, to eventually completely prove complex mathematical ideas.

If you wish to see other information beyond what the metamath-lamp explorer can show you, please look at the Metamath Home Page.

Proof: Principle of the syllogism (syl)

Let’s prove something much more basic. Let’s prove that if phi implies psi, and psi implies chi, then psi implies chi. In short, let’s prove that implication is transitive.

Russell and Whitehead call this claim “the principle of the syllogism”; others sometimes call this law a “hypothetical syllogism”. This has been proved in the set.mm database as theorem syl.

This proof involves using hypotheses, so that means we’ll learn how to create hypotheses in metamath-lamp.

Setting up the context and goal step for syl

As always, start up metamath-lamp.

If you’ve already been using metamath-lamp to prove something else, that means we need to erase the proof steps we have. Here’s how to do that:

Select the checkbox on the editor command icon bar above the field name “Description” to select all steps. Click on icon delete (delete) to delete all the selected steps. Long-click on the description text, delete all the text and click on save icon save (save).

If you already have a context, prepare to change the context.

At the top of the browser window, if you’ve already loaded a context you’ll see a icon expand more (expand more) drop-down arrow followed by “Loaded:…” text that hints at the current context. Click on that icon expand more (expand more).

Now select the new context.

Select Source type “Web”, alias “set.mm:latest”, and confirm it if requested. Change the scope to “Stop before” the label syl by typing it in and selecting it. Then press “Apply changes” to apply this change.

Setting up the description, goal, and hypotheses for syl

Let’s set the description.

Click on the field name “Description” to edit the description (you can also long-click on the area to its right where the text goes). Enter text like Prove syl. and press Enter (Return). Erase data for “Variables” and “Disjoints” if there are any (there probably aren’t).

Now let’s add the conclusion:

In the Editor select the icon add (add new statement). Enter |- ( ph -> ch ) and press Enter (Return). Long-click on the step label, change it to syl, and press Enter.

This statement isn’t always true; it’s only necessarily true when some other statements are true. In Metamath terminology these other statements are termed “hypotheses”. Let’s add some hypotheses.

In the Editor select the icon add (add new statement). Enter |- ( ph -> ps ) and press Enter. Metamath-lamp normally presumes that a new step describes a provable statement (that is, its step type is a “P”). However, this is a hypothesis instead. Long-click on the P on that line. On the drop-down drag down and select “H” (hypothesis) to change this step to a hypothesis. Notice that its justification is now “HYP” (it’s justified because it’s a hypothesis). Long-click on its label and rename it to syl.1.

We now have a hypothesis! Let’s add the other one:

In the Editor select the icon add (add new statement). Enter |- ( ps -> ch ) and press Enter. Long-click on the P on that line; on the drop-down list again select “H” (hypothesis). Again, its justification becomes “HYP”. Long-click on its label and rename it to syl.2.

Notice that it’s already ordered in a reasonable way. If you ever wanted to change the order of statements, you can select the step(s) to move using the left-hand-side check box, then use the icon up (up) and the icon down (down) to change their order. In this case, there’s no need to reorder these statements.

Note: Every hypothesis and goal label is also a database label, so they must be unique in the database they will be inserted into. These labels cannot match a math symbol token (like 1), assertion label, or hypothesis label. The convention in set.mm, as shown above, is for hypotheses to be labelled as the name of the goal + . + an integer starting from 1. Metamath-lamp validates labels you use (it currently validates hypotheses and will soon validate goals), and it will show an error message if the label is already in use in the current context.

Starting situation for syl

Here is what your display should look like at this point for proving syl:

Starting setup to prove theorem syl

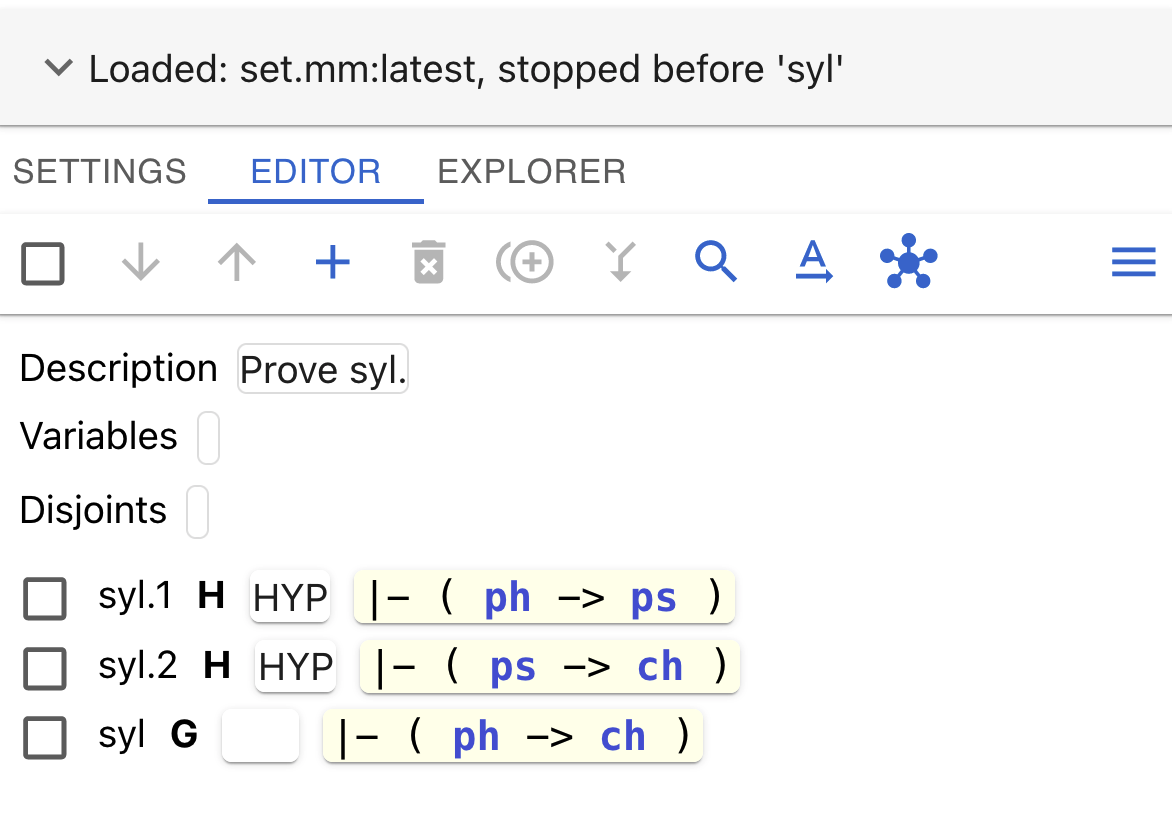
You can download this starting setup in metamath-lamp JSON format.

Easy proof of syl

Let’s prove syl the easy way. Metamath-lamp’s bottom-up proof tool can’t automatically prove all proofs, but it is able to find some proofs automatically, especially when it can use many theorems that have already been proved.

Select just the goal syl, and click on the icon Unify (unify). Press on “Prove”. The tool will soon reply with some options (you may need to scroll down to see them). These options will include, at or near the top, an option that uses imim2i and ax-mp that completely proves the claim. Select that one (using the checkbox on its left) and press on “Apply selected”.

Notice that metamath-lamp has added an intermediate step (with label “1”) to prove this :

|- ( ( ph -> ps ) -> ( ph -> ch ) )

Also, note that this new step and the final goal syl have green checkmarks.

The most important thing is that our final goal has a green checkmark, meaning the goal is fully proved! Here’s what the result looks like:

Screenshot of syl (easy proof)

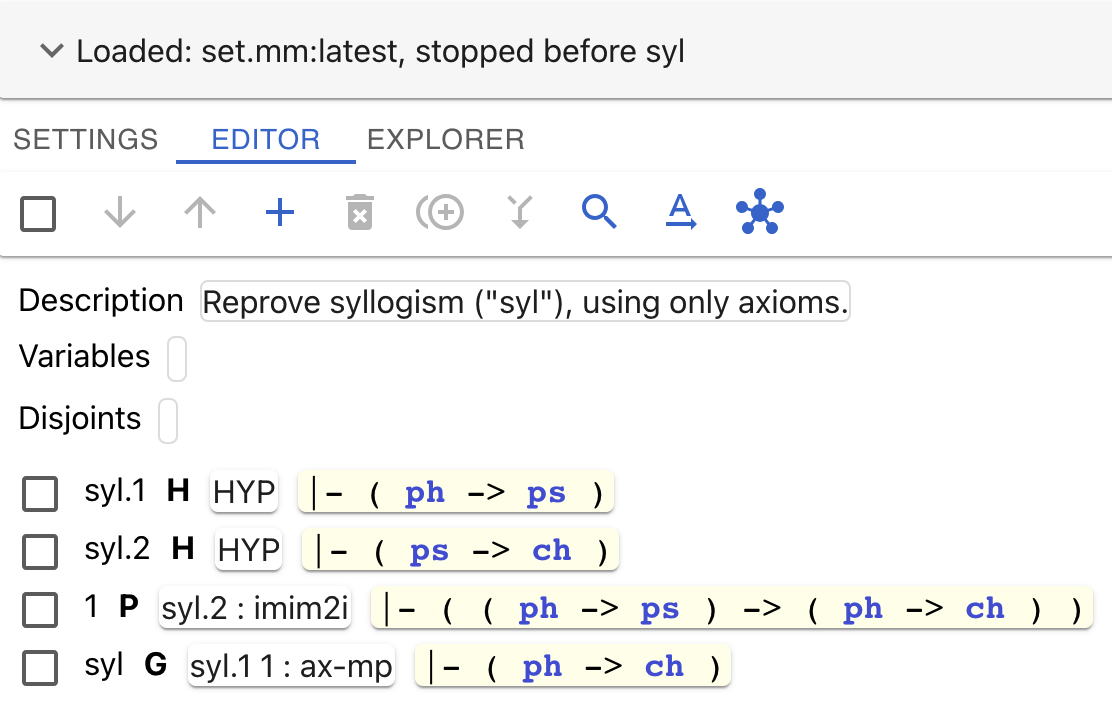
If you like, you can again extract the final compressed proof:

Click on the checkbox icon checkbox (select step) on the left of the goal step to select it. Click on the icon menu (menu), and select “Show completed proof”.

Hard mode: Proving syl using only axioms

If you thought that was too easy, let’s make it more challenging. Let’s prove syl using only axioms. Most people wouldn’t create proofs with only axioms, but some people find this to be an interesting challenge.

We’re going to create a proof using only axioms because this will help us illustrate ways you can use metamath-lamp. In particular, we’ll show you how to work backwards from a step.

Switch from our current state to hard mode

We’ll start with our current state, including the intermediate step that metamath-lamp found when we were doing things the easy way. Now change the context so that it includes the axioms modus ponens (ax-mp) and the propositional logic axioms ax-1, ax-2, and ax-3, and not anything after them:

Select at the top the context bar showing “Loaded:…” text. Change its scope to “stop after” label ax-3. Click “Apply changes”.

We now see an error after label 1, saying “The label ‘imim2i’ doesn’t refer to any assertion.”

The problem is that the justification of step 1 still says syl.2 : imim2i - this means that our claimed justification for step 1 was to use assertion imim2i with syl.2 as its hypothesis. In our modified context we can’t use imim2i, in fact, we can’t use any assertion after ax-3, including imim2i.

Let’s eliminate this justification:

Long-click on the now-invalid justification syl.2 : imim2i so that we can change it. We really just want to get rid of it, so click on the icon delete (delete) to delete the justification.

Let’s unify and see what happens (make sure all the steps are unselected before proceeding):

Click on the icon Unify (unify).

The final syl step has an orange “~”; this means that this particular step is justified on its own, but it transitively depends on something else that has not been justified. You can see that syl depends on two other statements, syl.1 and 1, and it uses ax-mp with those hypotheses to justify this step. This is a perfectly fine use of ax-mp, and syl.1 is a hypothesis (so it’s assumed true for its purposes). However, this justification depends on step 1 which isn’t currently proven.

What axioms are available in this situation?

We can use the explorer to view the axioms that we’re allowed to use in this “hard mode”. We don’t have much to work with!

We have modus ponens (ax-mp). Modus ponens (ax-mp) says that given some ph and ( ph -> ps ) then we may conclude ps.

We also have axioms ax-1, ax-2, and ax-3:

Axiom	Statement
ax-1	|- ( ph -> ( ps -> ph ) )
ax-2	|- ( ( ph -> ( ps -> ch ) ) -> ( ( ph -> ps ) -> ( ph -> ch ) ) )
ax-3	|- ( ( -. ph -> -. ps ) -> ( ps -> ph ) )

This system of modus ponens plus these three basic axioms is attributed to Jan Lukasiewicz (pronounced woo-kah-SHAY-vitch) and was popularized by Alonzo Church, who called it system P2. These axioms are widely used. If you want to know more about these axioms, see the Metamath book page 62 on.

That’s basically all we have. We did say this was hard mode. Let’s get started.

Working backwards on syl

Let’s work on proving step 1. Let’s try backwards proof.

Select step 1 by clicking the checkbox to its left. To start a backwards proof, click on the icon Unify (unify). Click on “Prove”.

The bottom-up prover will show us some options. It shows several ways to apply ax-mp (modus ponens), including cases where a hypothesis is directly used as one of the claims. Sometimes it’s not clear which alternative (if any) is worth trying, in which case, you may need to try out different approaches to see if they lead anywhere. It’s fine to try out different options; when creating a real proof, you often have to try different situations until you find one that works. As you do it you’ll get a better intuition for what is likely to work.

In this situation the direct applications of the hypothesis don’t look to me like they’re going to lead to a proof. So I’m going to select the option with a work variable &W1 because that seems more promising.

Click on the option that includes &W1 and use “Apply Selected”.

We haven’t seen work variables before; let’s explain them.

Interlude: Work variables

The symbols beginning with “&” are what’s called “work variables”. Work variables often show up when creating proofs. The fundamental issue is that although a theorem or axiom may use a variable (such as A), those variables can be substituted for other expressions of the same type when they are used. In cases where metamath-lamp cannot be certain of exactly what expression you want, it will create work variables that you can then substitute with whatever you do want (as long as they’re the same type).

When using set.mm or iset.mm, you’ll see work variables of certain types:

• &Wnumber : an expression that is a well-formed formula (wff), in short, some value that is true or false. This could be a variable that is a wff, such as ph (the ASCII representation for “𝜑”), ps (for “𝜓”), ch (for “𝜒”), or th (for “𝜃”). But it could be any other wff expression, such as ph /\ ps.
• &Cnumber : an expression that is a class. Any set is a class, though not all classes are sets. This could be a variable that is a class, such as A, B, C, and so on. It could also be an expression that is a class, such as ( sin ` A ).
• &Snumber : a set variable. This represents a variable that represents a set, such as x, y, or z. This can’t be an expression (class variables are used in this case). Set variables can show up immediately after quantifiers; requiring them to be a variable ensures that they are syntactically valid.

In work variables the number will increase from 1 as needed to keep different work variables distinct.

If you look carefully you’ll see that the “Variables” field in the proof display has new information once work variables are added. The “Variables” field shows a label, type, and name. The variables field is helpful when proofs get long, because it will show you in one place what work variables are not currently handled.

Metamath-lamp can export proofs with work variables (they will be treated like local variables and defined in the generated proof). However, many in the Metamath community would not accept this into a Metamath database, so in most cases you should change work variables to something else before exporting a proof.

In many cases you’d use the icon global substitution (global substitution) to replace the work variables with symbols or expressions so we can complete the proof.

Globally substituting some work variables

We now have these statements:

3  P  |- ( &W1 -> ( ( ph -> ps ) -> ( ph -> ch ) ) )
2  P  |- &W1

Statement 3 looks suspiciously like axiom ax-2, which states:

( ( ph -> ( ps -> ch ) ) -> ( ( ph -> ps ) -> ( ph -> ch ) ) )

Unfortunately, metamath-lamp’s current unifier doesn’t notice that these can be unified, so the bottom-up prover won’t help us here. The tool mmj2 can unify this statement with ax-2 because mmj2 currently has a more powerful unifier. Unfortunately, metamath-lamp’s current unifier is only unidirectional, that is, it can only substitute in one direction to find a match. In the technical literature the current metamath-lamp “unification” algorithm is often called “matching” instead of being considered full syntactic unification. There are some discussions about removing this limitation in metamath-lamp, but for now we’ll need to work around this limitation.

With a little extra work we can give metamath-lamp the information it needs. Let’s assume that we know we want to use ax-2 to prove this.

One approach would be to use global substitution to replace the work variable “&W1” with the expression required by ax-2, namely, ( ph -> ( ps -> ch ) ). Here’s how you could do that, but note that we’re going to cancel instead of completing this step:

Click on the icon global substitution (global substitution). In “Match what” use the value &W1 and in “Match with” use the value ( ph -> ( ps -> ch ) ) and then press Return (or click the “Find Substitution” button). Metamath-lamp will show one possible substitution. You could click on the “Apply button and then unify, but don’t; select the “Cancel” button instead.

That would have proven step 3 using ax-2. However, if the expressions were more complex and we had to take multiple steps, it might be hard to choose the correct substitutions.

A more general approach would be to add the step we want to use, so it’s easily seen in the editor, and then perform global substitutions until we can merge them together. This is a better approach for more complicated situations, because then the tool can help us see what we’re trying to accomplish and tell us when we succeeded. So let’s do it that way.

First, let’s bring in a step that uses the assertion we wish to use (in this case ax-2):

Click on the icon search (search), enter the label ax-2 and press “Search”. Select ax-2 and press “Choose Selected”.

We have added a new step 4, which uses ax-2 but with work variables:

|- ( ( &W3 -> ( &W4 -> &W2 ) ) -> ( ( &W3 -> &W4 ) -> ( &W3 -> &W2 ) ) )

We are now going to modify steps 3 and 4 until metamath-lamp can unify them. The key feature we’re going to use is that you can use the statement fragment selectors to simultaneously select two fragments, which may include multiple work variables, and then use global substitution. Global substitution will use the two selected fragments, making this process much easier.

Use a click to select, in step 4, the last ->.

If you didn’t pick the right fragment, click again to get the correct selection.

The statement fragment selector dialogue has appeared under step 4 and we now have this fragment selected:

( &W3 -> &W2 )

We want a slightly larger expression selected, and we can do that easily.

Click on the icon expand (expand selection) to expand the selected sequence of symbols.

You should now see this selected:

( ( &W3 -> &W4 ) -> ( &W3 -> &W2 ) )

Now let’s select the equivalent statement fragment in step 3:

Use a click to select, in step 3, the third -> (out of four).

Another fragment selector dialogue has appeared under step 3 and it has this fragment selected:

( ( ph -> ps ) -> ( ph -> ch ) )

If you didn’t pick the right fragment, click again to get the correct selection.

Note: you can select two fragments at the same time; you can also select two multiple statements. The ability to select two different fragments or two different statements simplifies global substitution.

Now we can use global substitution:

Select the icon global substitution (global substitution). The global substitution dialogue will appear, with our selections entered as the “Match what” and “Match with” entries.

The two selected fragments have been copied into the fields. The earlier selected fragment is the “Match what” and the later selected fragment is the “Match with” If they are in the opposition places of what you wanted, you can swap them by clicking on the icon reverse (reverse) on the right of the “Match what” field. In this case we don’t need to reverse anything, as this is what we want.

Click on “Find substitution”. Notice that it shows a valid substitution that replaces multiple work variables.

Again, notice that “Match what” doesn’t need to be a single work variable. It can be an expression, one that even includes multiple work variables. If there are multiple work variables, and you apply the change, all will be replaced as necessary throughout the proof.

Click on “Apply”. Notice that multiple work variables have been replaced.

We now have these two statements:

4 P |- ( ( ph -> ( ps -> ch ) ) -> ( ( ph -> ps ) -> ( ph -> ch ) ) )
3 P |- ( &W1 -> ( ( ph -> ps ) -> ( ph -> ch ) ) )

Now let’s do another global substitution to make steps 3 and 4 even more similar.

Use a click to select, in step 3, the initial work variable &W1 (only that work variable should be selected). Use a click to select, in step 4, the first ->.

The second long-click highlighted this fragment in step 4:

( ph -> ( ps -> ch ) )

Click on the icon global substitution (global substitution).

Again the two fragments are copied in. However, in this case the order is the opposite of what we wanted, because we want to replace a work variable with an expression (not the other way around). So we’ll swap them by clicking on the icon reverse (reverse) on the right of the “match what” field.

Click on the icon reverse (reverse) to swap the field contents, press “Find substitution”, then apply.

Handling the duplication in syl

Now both steps 3 and 4 are the same:

|- ( ( ph -> ( ps -> ch ) ) -> ( ( ph -> ps ) -> ( ph -> ch ) ) )

In fact, metamath-lamp is complaining that the two statements are the same! That’s not a problem, that’s what we were trying to do. Let’s merge them.

Select step 3 and click on the “merge” icon. Among the “use” options select using 4 (which uses ax-2), so we can keep the connection to ax-2. Step 3 is gone, now it’s all step 4. Click on the icon Unify (unify) to see we’ve fully proven step 4.

Completing syl in hard mode

We’re getting close! Step 4 is proven, using ax-2. However, step 2 is not yet proven, so the whole proof isn’t done. Select step 2, and do a bottom-up proof of it as well.

Select step 2, then click on the icon Unify (unify), and press “prove”. The tool will show various options for proving the result (you may need to scroll down). At the top it will show a use of ax-mp that proves all steps; select it and “apply selected”.

Congratulations! We now have a proof of syl by only using axioms directly.

Creating this proof by only using axioms lets us experiment with some features of metamath-lamp. That said, most of the time you won’t want to limit yourself to just axioms. Proofs are shorter, clearer, and easier to understand if you create theorems of more basic claims, and slowly build up from those simpler theorems to more complex claims. It’s also much easier to create each proof.

You can export this as JSON for later importing.

If you like, you can again extract the final compressed proof:

Click on the checkbox on the left of the goal step to select it. Click on the icon menu (menu), and select “Show completed proof”.

Screen shot of syl with only axioms

Here’s a screen shot of syl proven with only axioms.

Theorem `syl` proven with only axioms

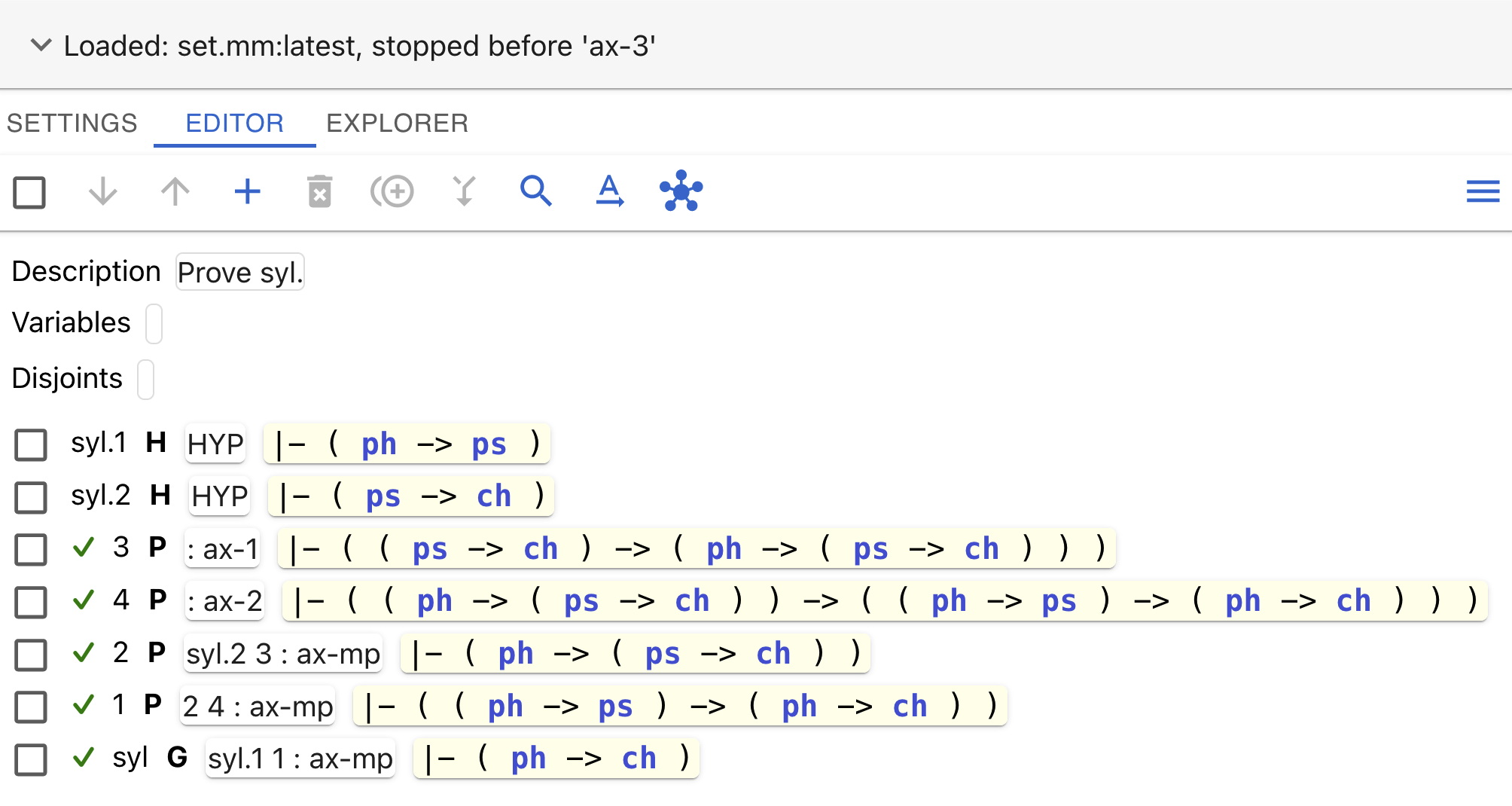
For your convenience, here is the axiom-only proof of syl in JSON format that you can download.

As noted earlier, there’s no mathematical reason you have to prove theorems using only axioms. But it can be a fun challenge, and this made it easy to demonstrate some of metamath-lamp’s capabilities.

Proof: The reciprocal of the cotangent is tangent (reccot)

Let’s use metamath-lamp to create another proof, namely, that the reciprocal of the cotangent is tangent. This has already been proved in the set.mm database as theorem reccot.

This exercise is based on the video showing how to prove the same theorem using the mmj2 tool (“Introduction to Metamath and mmj2” by David A. Wheeler) and an earlier video of reccot being proved using metamath-lamp (no sound).

Selecting the proof context for reccot

We first need to decide on the proof context, that is, the database(s) of axioms and proven theorems we’ll use. In this case we’ll again use the most common Metamath database, set.mm. We will again be proving something already in the database, so we need to make sure our context does not include its proof (of reccot) or metamath-lamp will just reuse it.

If you’ve already been using metamath-lamp to prove something else, that means we need to erase the proof steps we have. Here’s how to do that:

Select the checkbox on the editor command icon bar above the field name “Description” to select all steps. Click on icon delete (delete) to delete all the selected steps. Long-click on the description text, and click on its icon delete (delete).

If you already have a context, prepare to change the context.

At the top of the browser window, if you’ve already loaded a context you’ll see a icon expand more (expand more) drop-down arrow followed by “Loaded:…” text that hints at the current context. Click on that icon expand more (expand more).

Now change the context.

Select Source type “Web”, alias “set.mm:latest”, and confirm it if requested. Change the scope to “Stop before” the label reccot by typing it in and selecting it. Then press “Apply changes” to apply this change.

Setting the goal for reccot

For this example we’ll leave the proof description, variables, and disjoints blank. We do need to tell metamath-lamp our goal.

In the Editor select icon add (add new statement). Enter

|- ( ( A e. CC /\ ( sin ` A ) =/= 0 /\ ( cos ` A ) =/= 0 ) ->
    ( tan ` A ) = ( 1 / ( cot ` A ) ) )

and press Enter (Return) to save the result.

This is a more complicated goal. It says that if A is a member of the set of complex numbers, and the sine of A is not equal to zero, and the cosine of A is not equal to zero, then the tangent of A is equal to 1 divided by the cotangent of A.

Be sure to surround each symbol by at least one space (the first and last symbols can start and end the statement), and be careful about where the parenthesis go.

Now modify the label of this goal to reccot.

Select the step label (1) using the left mouse button. Change the step label to reccot and press Enter (Return).

Let’s take a brief look at this goal. It illustrates several symbols in the set.mm database:

• An uppercase letter like A represents a class (any set is also a class). By convention we start with A unless there’s a reason to do otherwise.
• CC represents the set of all complex numbers.
• e. represents “is a member of”; so A e. B is how we write “A ∈ B”. The expression A e. CC means “A is a complex number”.
• \/ represent “and”. It’s not used here, but /\ represents “or”.
• =/= represents “not equal to”.
• -> represents “implies”. The left-hand-side of an implication is called the antecedent; the right-hand-side of an implication is called the consequent.
• / represents complex number division.
• The form ( FUNCTION ` ARGUMENT ) applies function FUNCTION to ARGUMENT, that is, it determines the value of the function for that argument. Therefore ( tan ` A ) is the tangent of A. This left apostrophe notation originated from Peano and was adopted in Principia Mathematica by Whitehead and Russell, Quine, and others. This notation means the same thing as the tan(A) notation used by others but without context-dependent notational ambiguity.

See common set.mm symbols for more information.

Deciding on a proof strategy for reccot

Now we need to figure out how to prove this goal.

In this example our basic strategy will be to expand the tangent and cotangent into sines and cosines, then show that the results are equal. We’ll again show going forwards.

Note that in real proof efforts you’ll often try many different approaches.

Beginning to expand the definition of tangent

We know we’re going to need more information about the tangent and cotangent. So let’s retrieve their definitions.

Let’s first find the definition of the tangent.

Select the icon search (search). In the pattern enter ( tan ` and click on Search.

That produces a huge number of results. We could scroll through many pages to find what we want and select it. In this case, let’s instead be more specific in our search request. We want a statement that shows that the value of the tangent is equal to something using the sine and cosine.

While still in the search dialogue, modify the search pattern to say ( tan ` = sin cos and click on Search.

Notice that this more specific search quickly finds the definition we want without many irrelevant results. In this case it finds a statement named tanval (value of the tangent).

The default search pattern language is very simple. A pattern should consist of a space-separated sequence of one or more symbols (currently only constants and typecodes like class are allowed). Statements will only be considered matches if their conclusion part has the same constants in the same order, with optionally 1 or more other symbols before the pattern, between the requested symbols, and after the pattern.

This definition of the value of a tangent, named tanval, includes an implication. There’s a good reason for this. The tangent of some value A is the sine of A divided by the cosine of A, and therefore it’s undefined when the cosine of A equals zero.

While still in the search dialogue, select the box next to tanval. and press “Choose Selected”.

Interlude: Work variables in reccot

We have a new step, as expected. This one has work variables, in this case class work variables:

|- ( ( &C1 e. CC /\ ( cos ` &C1 ) =/= 0 ) ->
   ( tan ` &C1 ) = ( ( sin ` &C1 ) / ( cos ` &C1 ) ) )

We’ll need to globally substitute the work variables with other symbols or expressions to complete the proof.

Completing the work to expand the definition of tangent

We need to replace each work variable. What’s more, we need to replace them with an expression of the correct type that will help us eventually prove our goal. What should we do in this case?

In this case, the goal is going to involve the tangent of A, so we know we’re going to specifically need the tangent of A. Since we need ( tan ` A ) but we currently have ( tan ` &C1 ), we should replace all instances of &C1 with the value A. Metamath-lamp’s substitution command, chosen via the icon global substitution (global substitution), can help us do just that.

Select the icon global substitution (global substitution). In “Match what” enter &C1 and in “Match with” enter A and once that’s done, press “Find Substitution”. The system will check if this is valid; in this case, it determined that there was only 1 way to interpret this command and that the result is valid. As a result, metamath-lamp will show you that you can change &C1 to A - press Apply to apply the change.

Expanding the definition of cotangent

We also need the definition of cotangent. You may have noticed that the definition of the value of tangent was named tanval - that suggests a naming convention that we could use to make searching easier. In set.mm, the definition for finding a value of a function is usually the function’s abbreviated name followed by val. Let’s exploit that.

Select the icon search (search). In the label field (not the pattern field) enter cotval and click on the icon search (search). Select cotval and click on “Choose Selected”.

We again have a work variable, and we already know what its value should be, so let’s deal with that now.

Select the icon global substitution (global substitution). In “Match what” enter &C1 and in “Match with” enter A and once that’s done, press “Find Substitution”. It will show you that you can change &C1 to A so press Apply to apply the change.

What does reciprocal do?

The goal involves a reciprocal, so we need to find an existing theorem that proves “what a reciprocal does for me”. What I want to find is something like ( 1 / ( A / B ) ) = ( B / A ), which presumably will only be acceptable if A isn’t zero and B isn’t zero.

Select the icon search (search). In the pattern enter:

class =/= 0 /\ class =/= 0 -> 1 /

Now click on Search.

Searching produces a paged list of results. However, by giving a very specific search pattern we’ve narrowed the results to a short list to consider.

Notice the word class in the search. You can use a typecode in a search, which will then match any variable with the same typecode. In the set.mm database, class represents a class variable.

We could have found exactly what we wanted by being more specific, such as by using this pattern, but of course specific patterns are longer:

class =/= 0 /\ class =/= 0 -> ( 1 / ( class / class ) ) = ( class / class )

After looking at my options I find recdiv and that is what I want!

Click on the checkbox to the left of recdiv to select that step, then scroll to the bottom and click on “Choose Selected”.

Now we have two work variables, representing the numerator and denominator of the fraction being reciprocated. Notice that the “Variables” field lists these two variables.

We’ll come back to this in a moment.

Matching the goal’s antecedent for tangent

The goal is an implication; the antecedent of this implication has 3 requirements. However, the definition of the tangent value and cotangent value don’t exactly match the goal antecedent. We need to prove that we can use these values with the exact antecedents in our goal.

This will be easier to do if we duplicate an existing step and modify it.

Select the checkbox to the left of the expression using tan. Click on the icon duplicate (duplicate selected statement). This will create a copy of the selected step below the current step.

An easy way to modify the new step’s statement is to use metamath-lamp’s mechanisms for copying and pasting portions of text (aka “fragment selectors”).

Click on the second parenthesis of the goal statement. This will smartly select a syntactically complete portion of the statement and bring up a fragment selector dialogue below the statement.

In this case, we want to make a copy of the selected text in the goal, then paste that into the relevant section of the new statement.

Click on the icon copy (copy to clipboard) under the goal statement. Long-click on the second parenthesis of the new statement we just created, selecting its antecedent. Click on the icon edit (edit), then use your system’s paste command (“control-V” on most computers, “command-V” on Macintoshes) to overwrite the selected text with the text in the clipboard. On smartphones use a long-click in the selected edit region and select paste. Press Enter (Return) to save the modified statement.

We now have a new statement, showing value of a tangent is still valid given the antecedent of our goal:

|- ( ( A e. CC /\ ( sin ` A ) =/= 0 /\ ( cos ` A ) =/= 0 ) ->
     ( tan ` A ) = ( ( sin ` A ) / ( cos ` A ) ) )

It turns out that metamath-lamp can immediately prove this new step.

Click on the icon Unify (unify) in the editor command icon bar above the steps. Note that the new step now has a green checkmark.

Matching the goal’s antecedent for cotangent

Let’s do the same thing with the definition of the value of the cotangent, showing we can use this definition even given the antecedent of the goal.

Click on the checkbox to the left of the expression using cot. Click on the icon duplicate (duplicate selected statement). Click on the second parenthesis of the goal statement to select the antecedent of the goal.

Let’s copy this statement fragment into the clipboard.

Click on the icon copy (copy) under the goal statement. Now click on the second parenthesis of the new statement we just created, selecting its antecedent. Click on the icon edit (edit), then use your system’s paste command (“control-V” on most computers, “command-V” on Macintoshes) to overwrite the selected text with the text in the clipboard. Press Enter (Return) to save the modified statement. Click on the icon Unify (unify) to unify everything so far.

We now have several steps. All the steps are proved (have green checkmarks) except the goal statement.

Handling the reciprocal of the cotangent

Our goal is about the reciprocal of the tangent, not the tangent itself.

So let’s modify the definition of the value of the cotangent to show the value of the reciprocal of the tangent. Remember, in algebra you can do what you want on the left-hand-side of an equality, as long as you do the same thing on the right-hand side.

Select the checkbox on the left for the step with this statement:

|- ( ( A e. CC /\ ( sin ` A ) =/= 0 /\ ( cos ` A ) =/= 0 ) ->
     ( cot ` A ) = ( ( cos ` A ) / ( sin ` A ) ) )

Let’s duplicate this step. Click on the icon duplicate (duplicate selected statement). Long-click to edit it, and surround the left and right and sides of its equality with ( 1 / ... ) resulting in:

|- ( ( A e. CC /\ ( sin ` A ) =/= 0 /\ ( cos ` A ) =/= 0 ) ->
     ( 1 / ( cot ` A ) ) = ( 1 / ( ( cos ` A ) / ( sin ` A ) ) ) )

When you’re done, click on the icon Unify (unify).

Clearly we’re going to need to simplify the reciprocal of the cosine over the sine. We already have a step that does this, but we need to set its work variables appropriately.

If we were using mmj2, we could just edit one of the work variables, replace with its new value, and unify. Metamath-lamp doesn’t support this due to a known current limitation. Instead, metamath-lamp expects you to use the global substitution command. Let’s replace the work values so that they will work with this expansion of the reciprocal of the cotangent.

Let’s replace the work variable &C1:

Click on the icon global substitution (global substitution) to begin a substitution that will occur across the entire proof. In “Match what” enter &C1 and in “Match with” enter ( cos ` A ) … Once you’re done, press “Find Substitution”. It will determine that there is 1 valid substitution; press “Apply”.

Let’s replace the work variable &C2:

Click on the icon global substitution (global substitution). In “Match what” enter &C2 and in “Match with” enter ( sin ` A ) … once that’s done, press “Find Substitution”. It will determine that there is 1 valid substitution; press “Apply”. Click on the icon Unify (unify).

Again, all but the goal steps are proven.

Proving the preconditions we need

The statement where we replaced the work variables is at least now relevant, but its antecedent is not what we need - it’s not the same as the goal’s antecedent. We’ll need to show that the goal’s antecedent implies the antecedent of the statement we want to use.

For example, the goal says A e. CC (A is a complex number) but the earlier statement’s antecedent says ( cos ` A ) e. CC. Now, we know that if a value is a complex number, then its cosine is a complex number. Is this information already in the set.mm database? Let’s find out. Let’s look for that statement and, if it exists, add it.

Make sure no step is selected. Click on the icon search (search); enter the pattern e. CC -> cos e. CC and press search. You’ll see a list including coscl - select coscl and press “Choose Selected”. This has a work variable; click on the icon global substitution (global substitution) and replace &C1 with A (remember to select “Find Substitution” and then “Apply”). We now have |- ( A e. CC -> ( cos ` A ) e. CC ) as a statement.

We’ve noticed another naming convention in set.mm; a name ending in “cl” is often used to indicate a class. Let’s do it again.

Click on the icon search (search). Search for label (not the statement) sincl and search. Select sincl (not asincl!). Substitute &C1 with A (you should now know how to do that without detailed instructions about what to press).

We now have |- ( A e. CC -> ( sin ` A ) e. CC ) as a statement.

Now we can start simplifying the reciprocal of the division.

Select the step involving the reciprocal which has this long statement:

|- ( ( ( ( cos ` A ) e. CC /\ ( cos ` A ) =/= 0 ) /\
       ( ( sin ` A ) e. CC /\ ( sin ` A ) =/= 0 ) ) ->
     ( 1 / ( ( cos ` A ) / ( sin ` A ) ) ) =
       ( ( sin ` A ) / ( cos ` A ) ) )

Duplicate this step by clicking on the icon duplicate (duplicate selected statement). In the duplicate, change ( cos ` A) e. CC to A e. CC and once that’s done press Enter (Return). Click on the icon Unify (unify). Select that new step and duplicate it. In the duplicate step change its statement ( sin ` A ) e. CC to A e. CC, Press Enter, and click on the icon Unify (unify).

This antecedent of this latest new statement is still not exactly the same as the goal antecedent, but it’s very close. It’s likely the tool can easily complete that, so let’s create a new statement based on the one we just created but it has the exact same antecedent as the goal.

Select the latest new step with this (long) statement:

|- ( ( ( A e. CC /\ ( cos ` A ) =/= 0 ) /\
     ( A e. CC /\ ( sin ` A ) =/= 0 ) ) ->
     ( 1 / ( ( cos ` A ) / ( sin ` A ) ) ) =
       ( ( sin ` A ) / ( cos ` A ) ) )

Duplicate the step. Click on the second parentheses of the goal statement (so we can duplicate its antecedent) and click on the “copy” icon. Now click on the second parenthesis of our new statement, click on the icon edit (edit) below it, and paste with control-V (or command-V). Enter, then press the icon Unify (unify).

The unification worked!

In fact, that proved more than the new step. Now label reccot shows a green checkmark, which means we’ve completed the proof.

If you like, you can again extract the final compressed proof:

Click on the checkbox on the left of the goal step to select it. Click on the icon menu (menu), and select “Show completed proof”.

There are many other ways we could have proven this, and in fact, we could have done some of this with less manual work by more aggressively using backwards search. Many steps “simply worked” in this example, but there’s no shame in creating intermediate steps that aren’t instantly proved. If there are intermediate steps you need to prove to lead to the goal, just apply the same process - repeatedly work to prove those intermediate steps.

Exporting to URL and temporary mode (TEMP mode)

We can export this proof using “Export to JSON”. However, let’s briefly talk about an alternative, “Export to URL”.

Click on the icon menu (menu) on the top right of the display. Click on “Export to URL”

You can then share this URL, to easily share with others your current state. Anyone who opens this URL can see this state.

NOTE: When you open a URL exported this way, Metamath-lamp is opened in temporary mode (aka TEMP mode). Temporary mode is intended to let you view others’ work without erasing your own. Changes in temporary mode will not be stored to your local storage. That means closing a browser, closing its tab, or any internal error will erase the editor’s content. That’s why it is “temporary”.

To reduce the risk of accidentally doing something important while in temporary mode, the word “Editor” in the tab bar is shaded orange (warning you that editing is temporary) and the web page header starts with “TEMP”. Also, the first attempt to edit will remind you that you’re in temporary mode and that changes will be discarded later. You’ll see a message like this the first time you try to edit in temporary mode:

Editing in TEMP mode

You are about to edit in TEMP mode. All changes you do in TEMP mode will be erased upon closing current browser tab.

If you want to continue editing in regular mode, please do the following actions:

1. use “Export to JSON” to copy current editor state to the clipboard;
2. open a new tab (or switch to an already opened tab) with metamath-lamp in regular mode;
3. use “Import from JSON” to load the copied editor state from the clipboard.

There’s currently no mechanism to switch from temporary (TEMP) mode to regular mode. As noted in the warning, if you want to save results from TEMP mode, use “Export to JSON” to acquire the current state in JSON format. You can then use “Import from JSON” to load the results into a normal tab.

You can click on this link to open 2p2e4 in temp mode.

Creating your own examples from existing proofs

An excellent way to learn how to use metamath-lamp is to select a database (such as set.mm and iset.mm) and pick an existing proof in it. Then load the database and stop reading just before that proof. Try to create your own proof, consulting the known proof when you get stuck.

If you’re recreating an existing proof, and stop reading before that proof, you can (and in most cases should) reuse the same labels for the hypotheses and goal. The current context won’t include the labels of the proof you’re recreating, so metamath-lamp won’t complain about it. If you’re intentionally creating an alternative proof of the same goal, for eventual use in the database, then you do need to use different labels.

If you’ve already been using metamath-lamp to prove something else, that means we need to erase the proof steps we have. Here’s how to do that:

Select the checkbox on the editor command icon bar above the field name “Description” to select all steps. Click on icon delete (delete) to delete all the selected steps. Long-click on the description text, and click on its icon delete (delete).

If you already have a context, prepare to change the context.

At the top of the browser window, if you’ve already loaded a context you’ll see a icon expand more (expand more) drop-down arrow followed by “Loaded:…” text that hints at the current context. Click on that icon expand more (expand more).

Now change the context.

Select Source type “Web”, alias “set.mm:latest”, and confirm it if requested. Change the scope to “Stop before” the label you are proving by typing it in and selecting it. Then press “Apply changes” to apply this change.

Loading existing metamath-lamp proofs

You can use “import to JSON” to load worked examples of metamath-lamp.

For example, we have completed examples of these proofs available in JSON format:

• 2p2e4
• syl (easy version)
• syl (axioms only)
• reccot
• empty (import this JSON to erase everything)

You can also generate a URL that includes the proof state, and share that URL with anyone. When anyone views that URL, they will load that same state.

Notes about Metamath databases

As noted earlier, a Metamath database is a sequence of axioms and their associated proven theorems. The most widely supported Metamath database today is set.mm (classical logic with ZFC set theory), followed by iset.mm (intuitionistic logic with intuitionistic set theory), and others are available. Each database has its own conventions and notations. The set.mm and iset.mm databases share many conventions and notations, so we’ll focus on those.

The set.mm general conventions and set.mm label naming conventions document its various conventions to encourage consistency.

Let’s discuss a few specifics.

We mentioned earlier that set.mm is picky about the placement of parentheses. Let’s explain the rules in more detail:

• When a function that takes two classes and produces a class is applied as part of an infix expression, the expression is always surrounded by parentheses. For example, the use of “+” in ( 2 + 2 ).
• Predicate expressions in infix form that take two or three wffs (a true or false value) and produce a wff are also always surrounded by parentheses, such as ( ph -> ps ).
• In contrast, a binary relation (which compares two classes and produces a wff) applied in an infix expression is not surrounded by parentheses. This includes set membership, for example, “1 e. RR” (1 is a member of the set of real numbers) has no parentheses.

The set.mm label naming conventions page discusses those conventions in more detail. In most cases, the name of a theorem is a concatenation of “label fragments” of the important part of its conclusion. Each label fragment as a meaning, e.g., “nn” for natural numbers, “re” for real numbers, “1” for the number 1, “gt” for “greater than”, “le” for less than, “an” for the boolean operation “and”, and so on. The label naming convention for a simple arithmetic expression is to use “p” for “plus” and “e” for “equals”. Most symbols are defined by an assertion named “df-NAME”, where NAME is the label fragment used. Note that in set.mm, “natural number” means an integer that is one or larger.

Thus, in set.mm, nnre represents “the natural numbers are real numbers”, nnge1 represents “the natural numbers are greater than or equal to 1”, and 2p2e4 represents “two plus two equals four”.

If you intend to add theorems to the set.mm database, you might find it useful to look at the Metamath Proof Explorer (set.mm), including its pages on Real and Complex Numbers, Algebraic and Topological Structures, and Deduction Format and Natural Deduction. There is a Complete symbol to ASCII Correspondance page. As explained in Deduction Format and Natural Deduction, many theorems are expressed in “deduction form”, where all hypotheses (other than definitions) have the form ( ph -> ...) and the conclusion is also in the form ( ph -> ...).

Conclusion of this user guide

This is the end of the user guide / tutorial portion of this guide. We hope you’ve found it helpful.

If you need more help on using the metamath-lamp tool or how to create proofs, the best place to go is probably the Metamath mailing list. We’d love to see more people creating proofs and getting them into Metamath databases! There’s a lot to learn, but we would be delighted to help.

Reference manual

This is the reference manual portion of this guide. In this portion we will walk through various portions of the metamath-lamp user interface to help you understand how to use it. That includes some capabilities that might not be obvious.

Here we will discuss:

• Basic UI conventions
• Loading source Metamath databases to create the proof context
• Main tabs: Settings, Editor, and Explorer
• Editor tab
• Settings tab
• Explorer tab
• Individual Assertion tab
• Temporary mode (TEMP mode)
• Common set.mm symbols
• Metamath-lamp update history

Basic UI conventions

A click, aka a short click or short tap, lets you select a button, reveal information, toggle a display, or select some information.

In this document we use the term “click” to mean either a click with the left mouse button or a tap on a touchscreen. A click with a mouse involves moving the mouse cursor to point to the object to be manipulated, pressing the left mouse button down, and then immediately releasing the left mouse button. A tap on a touchscreen is considered equivalent to a click; it involves briefly pressing the object on the screen and immediately releasing the press.

Edits generally require a long-click by default. There are multiple ways to do a long-click. Using a mouse, you can press down on the mouse, wait a second, then release. Using a touchscreen, you can press down on the screen, wait a second, then release. With a mouse you can also use a shortcut: hold the Alt key (sometimes labelled Opt or Option instead), then click with the mouse.

There are various shortcuts. You can use the settings tab so that on statements the meaning is swapped, that is, a click edits the statement and a long-click enables statement fragment selection.

Also:

• To save an edit, click on the icon save (save) or press Enter (Return).
• To cancel an edit, click on the icon cancel (cancel) or press Esc (Escape).
• To delete something selected, click on the icon delete (delete).

Loading source Metamath databases to create the proof context

Before creating a mathematical proof using metamath-lamp, you must first load at least one Metamath database and decide how much of those database(s) to use. This creates the context of a proof - that is, the set of axioms, proven theorems, and so on that the proof is allowed to use.

One of the powerful benefits of the Metamath system is that it does not impose any particular set of axioms (such as those of logic or set theory). However, to create a proof, you need to start with some set of axioms, and typically you’ll want to build on other proofs that use those axioms. So we must first tell metamath-lamp what this proof is allowed to use, aka the context.

The context is shown at the top of the UI. When metamath-lamp starts, it will tell you that no database/context is loaded. Select the “source type” of the database, which is:

• “web” - load from the world wide web. You then need to pick an alias (which database on the web).
• “local” - load from a local file. You then need to choose the file.

Most users will just choose “web” and use “set.mm:latest”. This is the current version of set.mm (aka the Metamath Proof Explorer), which is based on classical logic and ZFC set theory. This is the largest Metamath database.

Confirm as necessary. Once it’s loaded, you’ll need to pick a scope. A Metamath database is a sequence of statements, and metamath-lamp will only let you use statements that are in scope. The scope options are:

• “Read all” - use all statements in the source.
• “Stop before” (label) - use all statements up to but not including the given label. If you want to practice re-proving some statement, use this and give the label of what you want to prove yourself. Trying to prove something already proven is a great way to learn how to use metamath-lamp.
• “Stop after” (label) - use all statements up to and including the given label. If you want to use statements up to some label and not beyond, this is how to do that.

You can select the icon add (add) to add another source, and the adjacent icon delete (delete) to remove a source. In most cases you won’t load another source. A common use for adding another source is if you’re using a public Metamath database as a starting point, but have your own private collection of definitions and proofs in your local file storage.

Once you’ve selected all sources, select “Apply changes” to process these source databases. After it’s applied, the source selection section is hidden and you can start creating a proof with the proof editor.

Main tabs: Settings, Editor, and Explorer

Once you’ve loaded the context, at the top there is a tab bar with three tabs:

• The “Editor tab” is the main view that lets you see and edit a proof.
• The “Settings tab” lets you change the editor configuration to your liking,
• The “Explorer tab” lets you view the current context, e.g., the axioms and theorems.

There may also be dynamically-created individual Assertion tab.

Click on the name of the tab that you wish to see, and that tab will be displayed below it. We’ll cover the Settings tab later; let’s first focus on the Editor tab.

Editor tab

The Editor tab lets you edit a proof; it starts empty. You will create a list of statements in the editor that will eventually result in a proof. This tab contains most of the tool capabilities, so there’s a lot to discuss here.

We’ll first cover its key UI capabilities from top to bottom, starting from the editor command icon bar. We’ll then discuss how to state the goal and hypotheses. We complete this section with detailed descriptions of some of the more complex dialogues in the editor tab. Here is the full list of subsections:

• Editor command icon bar - this is the topmost area in the editor tab, a bar with icons representing commands to modify the proof
• Fundamental proof information - this is the region under the editor command icon bar for the description, variables, and disjoints.
• List of steps in the proof
• Fragment selectors - for selecting parts of a statement in the list of statements.
• How to state the goal and hypotheses - a summary of how to do this.
• Search patterns
• Global substitution
• Proving bottom-up
• Unification

Editor command icon bar

At the top of the editor tab is the editor command icon bar. This is a bar containing icons, where each icon represents a command that can be performed to modify the proof. You can hover over an icon to see what the command does. Here are their icons and meanings:

Icon	Meaning	Visual Description	Additional information
checkbox	Select all	Checkbox	Select or deselect all current steps
down	Down	Down arrow	Move the selected steps down the list
up	Up	Up arrow	Move the selected steps up the list
add	Add new statement	Plus sign	Type in the new statement
add	Delete selected steps	Trash can
duplicate	Duplicate selected statement	Circles behind “+”	Makes a copy of the selected statement
merge	Merge similar steps	Merge	Select one statement
search	Search	Magnifying glass	Add new steps by searching for a pattern; see search patterns
global substitution	Substitution	A with arrow	Apply a global substitution (aka replacement) to all statements in the proof; see global substitution
Unify	Unify	Hub	Unify all steps or unify selected provable bottom-up. If no steps are selected, attempt to unify everything. If one statement is selected, open proving bottom-up dialogue
menu	Menu	3 horizontal lines aka hamburger	Menu of other actions

Under the editor command icon bar is the fundamental proof information followed by the list of steps in the proof. After discussing the list of steps in the proof we’ll discuss fragment selectors, which let us easily select parts of a statement. We’ll then discuss how to state the goal and hypotheses. This will be followed by detailed discussions about some specific commands (how to specify search patterns, global substitution, and proving bottom-up).

Fundamental proof information

Just under the editor command icon bar is fundamental proof information, specifically fields for its description, variables, and disjoints. You don’t need to fill in a description or variable list to begin a proof. In many cases you won’t need to specify disjoints for a proof either, but sometimes you do. Here is information on these fields.

As always, you can long-click on the field to edit it.

There is a shortcut for these fields. You may also click on the field name to edit the field.

Description

This is a description of the proof. This description is included as a comment in the generated proof.

If you are following the conventions of set.mm, the first sentence of the description should be an English sentence explaining what is being proved. Surround Metamath statements with backquotes (so they can be typographically formatted) and precede references to another with an isolated “~”. Conventionally the description includes, at its end, text like “(Contributed by NAME, DD-MMM-YYYY)” where DD-MMM-YYYY is the date the proof was completed and MMM is the 3-letter English name of the month.

Work and Local Variables

This section shows a list of work variables and local variables, one variable per line. By default any variables no longer in use are removed.

Whenever a new work variable is created it will be shown in this list. Whenever a work variable is removed (e.g., by substituting it), it’s removed from the list.

If you’d like to give a variable a “local” name in the proof to make the proof clearer, you can do that by editing this field. You simply add a line with this format:

.NEW_LABEL TYPE VARIABLE_NAME

The “type” depends on the database, e.g., in set.mm it could be class, wff, or setvar. An example would be:

.loc1 class width

Notice the “.”. The period suppresses automatic deletion of the line; without it, if the variable is unused then entry will disappear.

Once a local variable is defined, you can use its name instead of the global name.

If you generate a proof that uses the local variable name, the local variable is exported as part of the proof. If you don’t want to export the local variable, you can replace the local variables with global variables before generating a proof.

Disjoints

The disjoints field presents a list of disjoint variables, one disjoint expression per line. A disjoint expression (a text line) must be a list of two or more variables separated by commas. Disjoint variables are also called distinct variables.

An example of a disjoint field’s contents might be this list, representing three disjoint expressions:

x,y,F
x,y,u,v

The disjoint expression x,y simply means that x and y must be disjoint variables (aka distinct variables). This means that they may not be simultaneously substituted with the same variable. The disjoint expression x,ph means variable x must not occur in the wff ph.

For more information, see the Metamath book.

List of steps in the proof

The list of steps of the proof follows the basic information about the proof.

By default, when the tool begins there will be no steps. Typically the first step to be added is the step to be proved (aka the goal step). Use the icon add (add new statement) in the editor command icon bar to add the goal. Usually the goal is the last step, though metamath-lamp does not enforce this.

Each step is presented in the following left-to-right order:

• Box (step selector): Select this box to select or unselect this step. Many commands work on the “currently selected step(s)”, so it’s important to be able to easily select steps. Click on the step’s box to select or unselect it. Use the box up in the editor command icon bar to select or deselect all steps.
• Proof readiness status (if present): If there’s a green checkmark following the step selector box, a recent unification has confirmed that this step is completely (transitively) proven given its context, justification, and previous steps. If there’s an orange “~” (tilde), the step itself has a valid justification but it transitively depends on something that is not proven. Any modification of a proof removes the proof readiness status. To regenerate the proof readiness status, press the icon Unify (unify) without selecting any particular step; this will re-verify the steps. If you see a green checkmark or orange “~” you can click on the symbol to show its visualization. If you see a green checkmark you can long-click on it to show its compressed proof (you can also select the step and use the menu option “Show completed proof”). Once you view a completed compressed proof you can show or hide the proof table. If you show a proof table you can decide if should only contain essential steps. Non-essential steps are the steps showing how to create syntactic structures and show that they are of the correct types. Metamath-lamp can export proofs with work variables (they will be treated like local variables and defined in the generated proof). However, many in the Metamath community would not accept work variables into a Metamath database, so in most cases you should change work variables to something else before exporting a proof.
• Label: This is the label for this statement. You should give your proof’s goal the label of what you intend to name it. Consider using the label “qed” for the goal step if you don’t know what name to use. Each hypothesis and the goal needs to have a unique label that isn’t already in the context being used (it can’t be a math symbol, label, or anything else). These labels (of the hypotheses and goal) are called “global labels”; the other labels in the proof are “local labels”. If you’re following the conventions of set.mm, the name of each hypothesis is the goal name followed by a period and an integer (starting with 1). For example, the proof of mp3an3an might have hypotheses with labels mp3an3an.1 and mp3an3an.2. Note that this is different from the convention of the mmj2 tool, where hypotheses have labels of “h1” and so on. All other step labels (the “local labels”) are typically consecutive integers starting with 1, though they don’t need to be; a local label can be any sequence of alphanumeric characters. Again, if you want to add a generated proof to a Metamath database, the label of every hypothesis and goal must not already be used. The point of a label is to provide a simple way to uniquely refer to a statement.
• Step type (P/H/G): The step type is “P” if it’s a provable statement (a statement to be proven), “H” if the statement is an (essential) hypothesis, or “G” if the statement is a goal (a special kind of provable statement). Typically all hypotheses are listed first and the goal is shown last. for the proved step (if any). Use click to reveal the justification (if it’s hidden). Use long-click to change (edit) the step type.
• Justification: This justifies why some statement is true. For hypotheses this is “HYP”. For provable and goal statements, this has the form “hyps:ref”, where hyps is a space-separated list of previous step’s labels that are being used in the justification and ref is a reference to an axiom or theorem in the current context.
• Statement: This is the statement to be proven or is being accepted as a hypothesis. In most cases this statement will start with |- (meaning “it is true that…”), followed by a space-separated sequence of symbols of the statement to be proved. An example of a statement is |- ( 2 + 2 ) = 4 (two plus two equals four). You can edit the statement. By default, you can do this by clicking on the text with the mouse left button or by touching it using a touchscreen. Once you’re done, press the icon save (save) to save the edited statement, or the icon cancel (cancel) to not change the statement. You can also select parts of a statement; see the next section on fragment selectors.

Fragment selectors

It’s very common when creating a proof to want to copy part of a statement. Therefore, metamath-lamp has mechanisms to make selecting parts of a statement very easy, especially in the presence of parentheses-like constructs. This mechanism is called a fragment selector.

By default, clicking on a symbol in a statement causes a fragment selector dialogue to appear and makes a selection based on the selected symbol.

Exactly what fragment is selected depends on the symbol you choose. If you select a parentheses-like symbol, it selects the expression that begins or ends with that symbol. If you select an infix relationship symbol, it selects the expression immediately surrounding the infix symbol.

Once you select a fragment you can change selection. Clicking on the icon expand (expand selection) will expand the selected sequence of symbols, while the icon shrink (shrink selection) will shrink the selected sequence of symbols.

Here is the full set of icons in the fragment selection bar:

Icon	Meaning	Visual Description	Additional information
expand	Expand selection	Zoom in	Expand the selection to the next larger syntactic unit
shrink	Shrink selection	Zoom out	Reduce the selection to the next smaller syntactic unit
add above	Add new statement above	Arrow up from box	Create a new step above the current step with the selected statement fragment
add below	Add new statement below	Arrow down from box	Create a new step below the current step with the selected statement fragment
copy	Copy to clipboard		Copy the fragment into the clipboard
edit	Edit	Pencil	Start editing with current text selected
cancel	Cancel	Circled X	Cancel (and close) this statement fragment dialogue

Important: You can use a fragment selector on more than one step at the same time. In particular, you can use the fragment selector on two statements and then invoke global substitution. Both fragments can be complex expressions when global substitution occurs (they are not limited to single symbols or only one work variable).

How to state the goal and hypotheses

To prove something, you must first tell the system what to prove and any special hypotheses to use. To do that:

• Under the “Editor” tab”, press the “+” in the editor command icon bar to create a new statement. Enter the goal of the proof as its statement. Typically the goal’s statement will begin with the symbol “|-“ which means “it is true that”. Click on its step number if you want to rename the step name (typically this is named “qed” if you don’t have a better name). By default the step added when there are currently no steps is assigned the step type G (goal) - a special kind of provable statement that by default is kept at the end of the list of steps.
• If there are (essential) hypotheses, click on the icon add (add new statement), enter the statement text, and then long-click on the P. Change “P” (provable assertion) into “H” (hypothesis). (Note: In this document, unless we specifically say otherwise, when we say “hypothesis” we mean a Metamath essential hypothesis). Put them in the intended order by selecting them (the box on the left) and clicking on the up and down icons. You may want to rename the labels of the hypotheses.

You’re now ready to create a proof.

Important: The label of every hypothesis, as well as the goal, is a database label. Therefore these labels must be unique in the context. The label cannot match a math symbol token (like 1), an assertion label, or a label of any other hypotheses. This is noted in the Metamath book, page 114, as it notes that “each label token must be unique, and no label token may match any math symbol token.” The convention in set.mm is for hypotheses to be labelled as the name of the goal + “.” + an integer starting from 1. Note that the label of individual proof steps (other than the hypotheses and goal) don’t have to be unique in the database, because these labels are local to the proof.

Let’s now look at details of some of the more complex dialogues in the tools

Search patterns

The icon search (search) enables you to search for a statement that matches a given pattern, showing you matches. You can then select a match and create a new statement from that match.

The search pattern language is very simple, Note that search will only match on the conclusion part of an axiom or theorem (there is currently no mechanism to search hypotheses).

A pattern must be a space-separated sequence of one or more items. Each item must be a constant or a typecode that is valid in the database:

• A constant pattern only matches the same constant.
• A typecode pattern matches any variable with that typecode. For example, in the set.mm database, the valid typecodes you can use in a pattern are wff (which will match variables like ph and ps), class (which will match variables like A and B), or setvar (which will match variables like x and y)..

Statements will only be considered matches if their conclusion part has the same matching symbols in the same order. There may be 1 or more other symbols before the pattern, 1 or more symbols between the requested items, and 1 or more symbols after the last matched item.

Therefore, a search for 0 -> will match the conclusion |- ( ( 0 <_ A /\ 0 <_ B ) -> 0 <_ ( A + B ) ) because the conclusion has a 0 constant which is later followed by a -> constant.

Global substitution

Click on the icon global substitution (global substitution) to replace one expression with another expression across the entire proof.

This global substitution will be applied to all statements in all proof steps!

After you select this icon you’ll be presented with a simple dialogue box to describe the global substitution:

• In the “Match what” field, enter what expression you want to change, (e.g., &C1 or ( &W1 -> &W2 )).
• In the “Match with” field, enter what expression you want the first expression to change into (e.g., A or ( ph -> ch )).

You can use fragment selectors to select one or two statement(s) before starting a global substitution. When you press the global substitution icon, a copy of the first fragment (in displayed order) will be placed in the “Match what” field, while a copy of the second fragment (if any) will be placed in the “Match with” field. You can use the icon reverse (reverse) to swap the field entries.

You can also use the checkboxes on the left to select steps before starting a global substitution. The steps selected first will be copied into the “Match what” field, and the step selected second (if any) will be copied into the “Match with” field.

When you press “Find Substitution” the tool will determine if it can apply this substitution (that is, if the results are valid types everywhere and there are valid substitutions) across the prof. If it is valid, you may select “Apply” to apply it.

Important: Global substitutions are not limited to a single symbol. Both fields can be complex expressions, possibly including more than one work variable. The tool allows you to use fragment selectors to select expressions to easily substitute one complex expression with another.

Proving bottom-up

If you select one statement and then select unify, you’ll enter a “proving bottom-up” dialogue. The bottom-up prover does a breadth-first search to find a proof of the selected statement backwards (bottom-up) using the current context and the options set in this “proving bottom-up” dialogue.

It essentially works backwards to find a match, first with a single level, then with 2 levels (a statement that depends on another that also requires proving), and so on. It will stop once it finds a proof. In this version it uses no heuristics, and simply tries all allowed options as specified in the dialogue.

Typically you would modify the search options shown in this dialogue box and press “Prove” (or “Cancel” if you don’t want to search). When you press “Prove” it will repeatedly attempt various options in an attempt to prove the statement, showing the depth of the current search (e.g., “1/4” means it’s doing depth 1 searches out of a maximum of 4) and how many attempts it’s made so far. Click on the circled “X” to stop its attempts to find a proof.

Proving bottom-up can take a long time, depending on the problem and the speed of the computer. The options selected here will affect whether or not it can find a proof and the time it takes to do it. Therefore, selecting the right options for your circumstance in the proving bottom-up dialogue box can be very important. So first, let’s understand what it does

How bottom-up proving works

We can imagine the search space growing as a tree from the bottom, starting with the statement we wish to prove. All the statements we used to directly try to prove the current goal are considered “depth 1”. If those won’t work directly, we can try each depth 1 statement and then retry with many more statements, and so on. The following figure illustrates this

Bottom-up proving starting up from the statement to prove

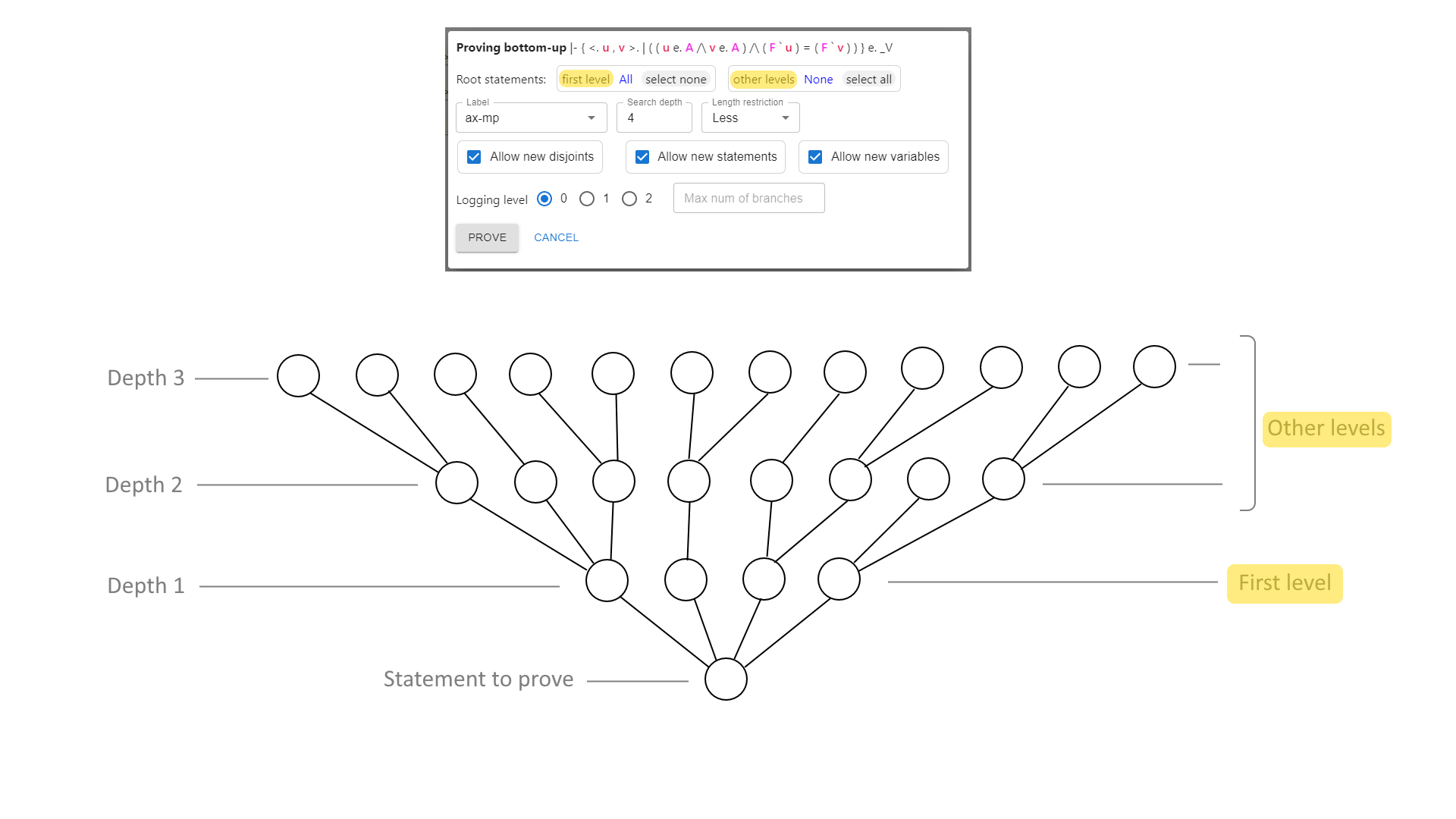
The “search depth” defines the maximum depth of the search. For example, the following figure shows the search space if the search depth is 2; the prover will stop searching once these options are exhausted:

Bottom-up proving is limited by search depth

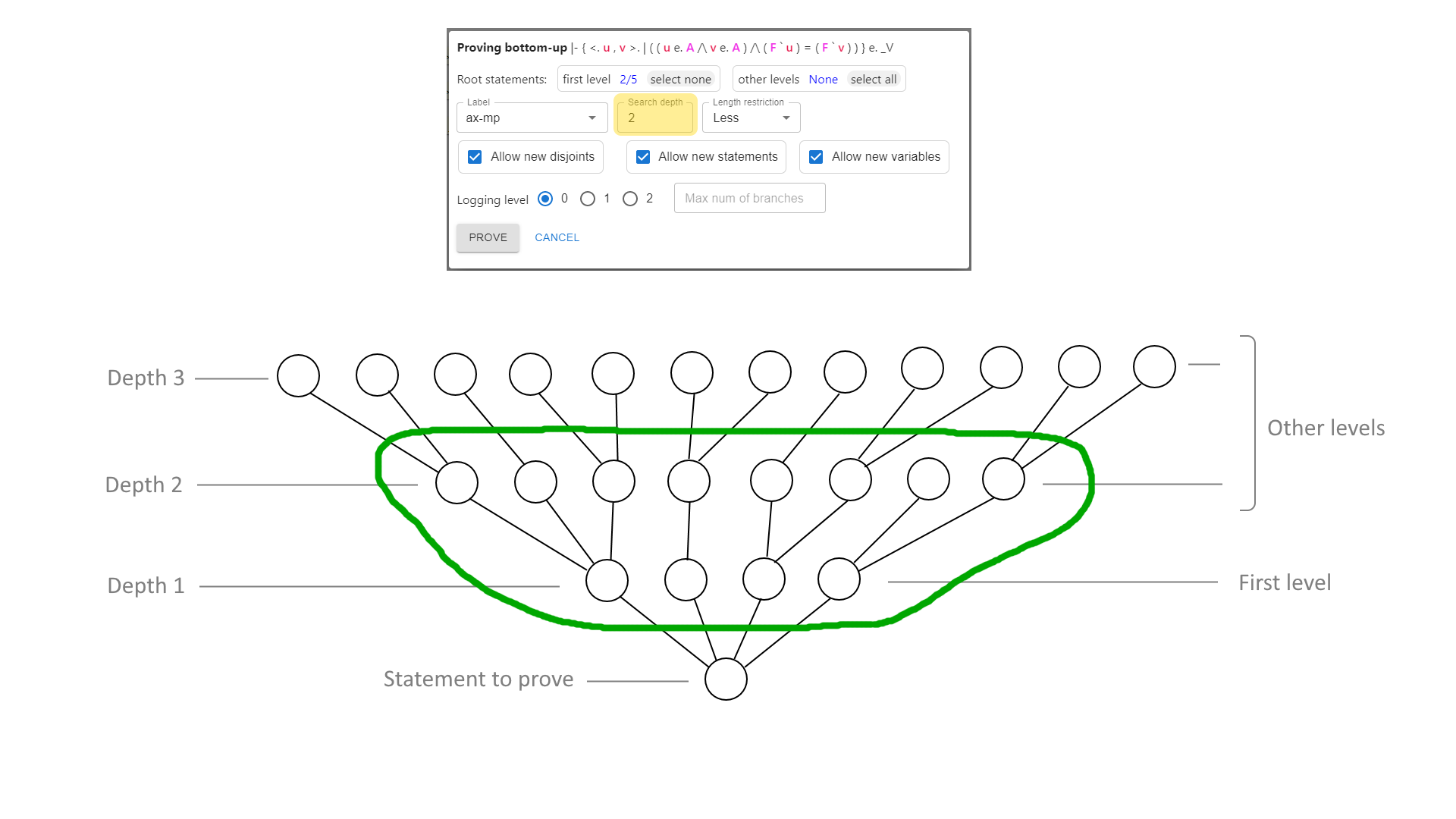
The “label” setting tells the prover to only use the given label at the first level; it has no effect on other levels:

Bottom-up proving will only use the selected label if specified

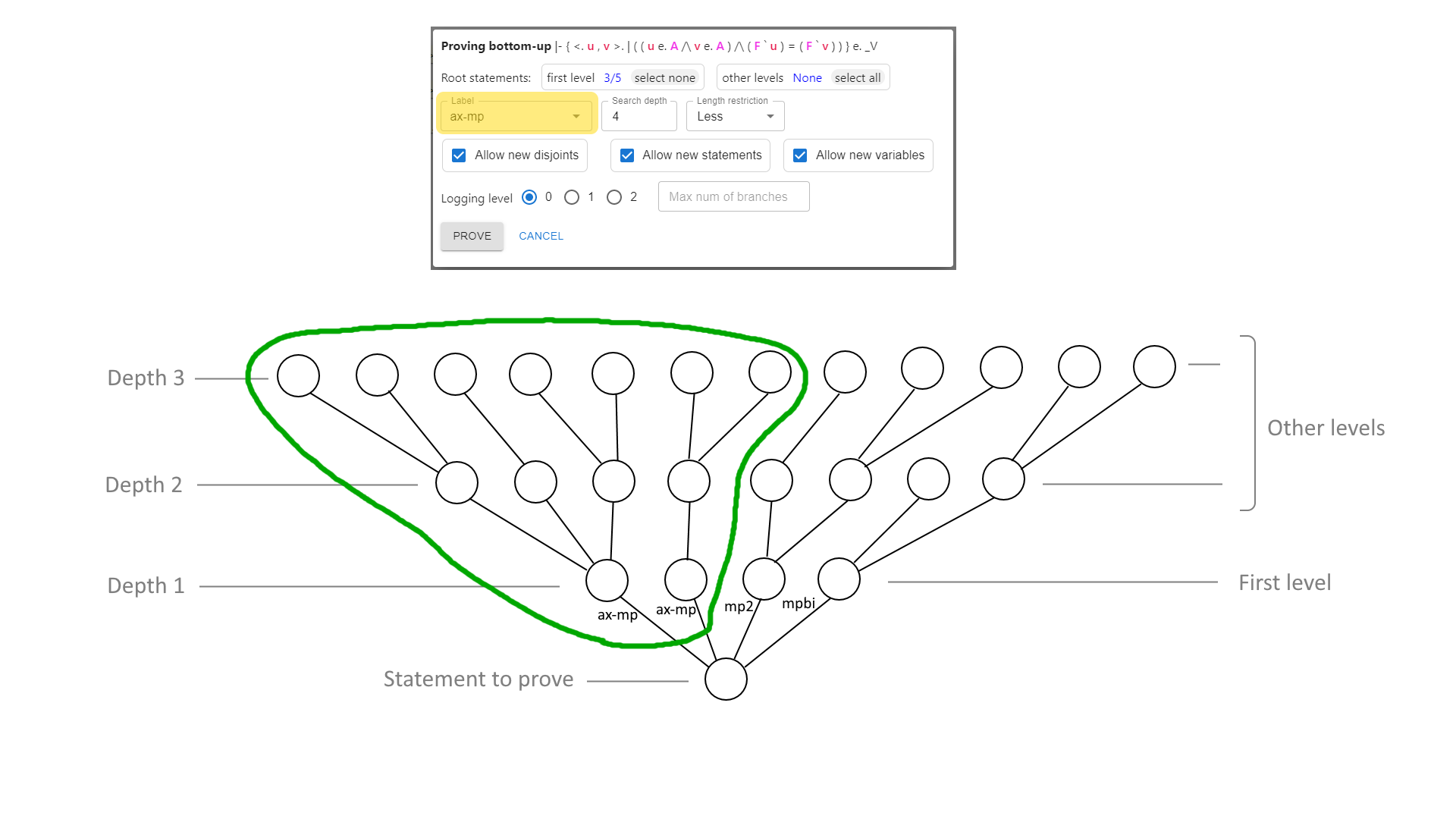
The “length” setting restricts which statements are considered based on their length. This setting is ignored on the first level. Let’s assume that statement A is derived from statement B and the “length” option is set to “Less”. The prover will only consider statement B if the length of statement B is less than the length of statement A. This heuristic can speed searches. The rationale is that a supporting statement is more likely to be useful if it is simpler, not more complicated, than the statement it supports. This figure illustrates the situation:

Bottom-up proving with the "length" setting compare the lengths of a statement and its supporting statement

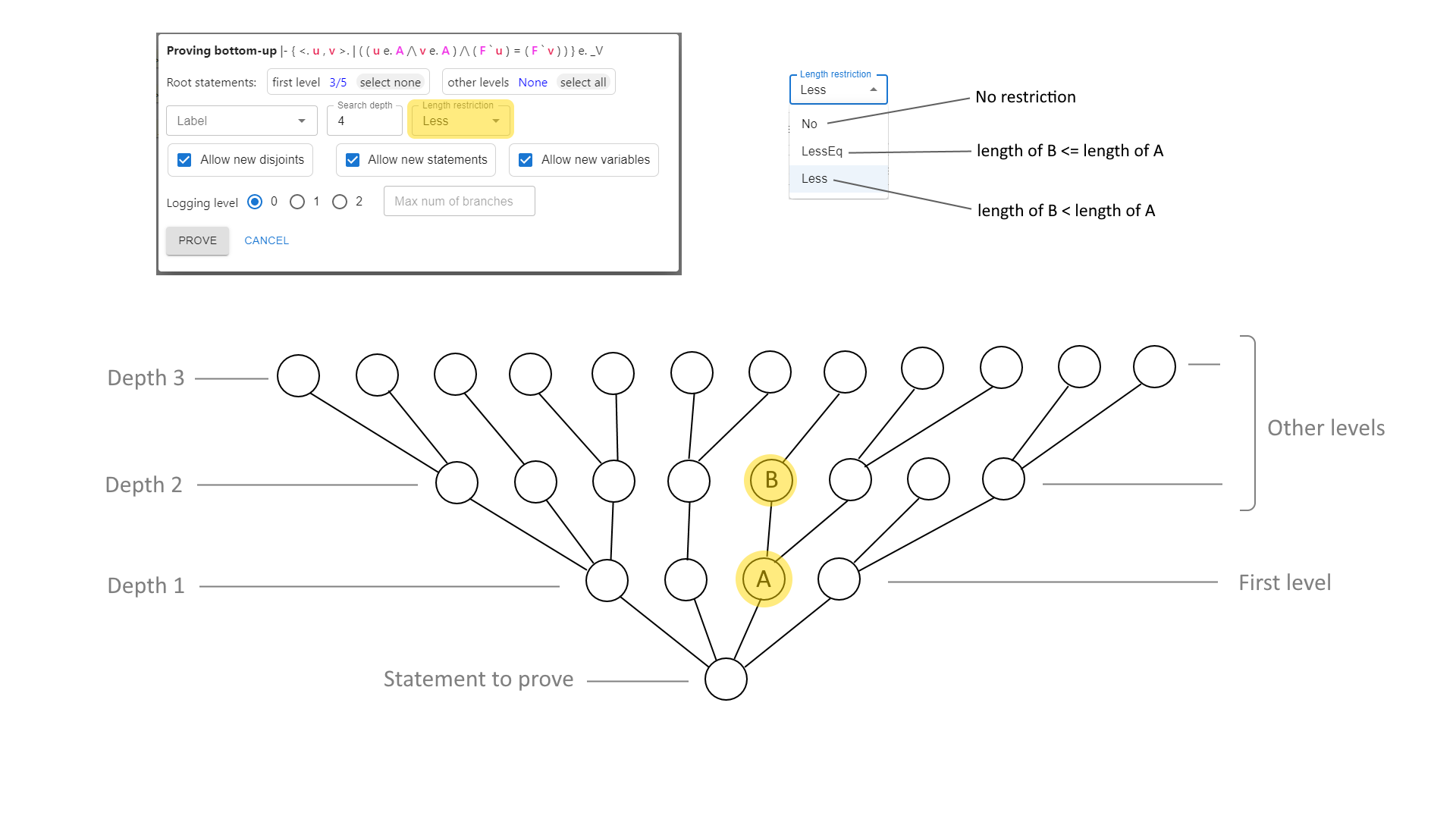
Now that we understand how bottom-up proving works, let’s review its dialogue box options.

Proving bottom-up dialogue box options

This dialogue has the following options:

Root statements (“first level” and “other levels”): These let you select which steps (if any) currently in the proof may be used (that is, derived from). If a statement isn’t selected it will not be considered when creating the proof. The “First level” option selects the steps that may be used to directly prove the root statement being proved, while “other levels” selects the steps that may be used beyond this level. We can select “all” (all steps may be used), “none” (no steps may be used), or select a specific set of steps that may be used. If it shows an expression like “1/8”, that means a specific set of steps have been selected; the first number is the number of steps that are permitted, and the second number is the number of steps that could be permitted at this point. Click on the current value to select the steps to permit. If the statement to be proved is not currently proved, the “first level” is set to “All” (all steps are considered) and the “other levels” is set to “None” (no steps are considered after the first level). If this statement is already proved, the “first level” will be set to the steps that were used. Adding steps that can be used will increase what the bottom-up prover can prove, but this will also increase the time it takes to find a proof.

Label: If set, this is the label of the only reference that is allowed to be used as a starting point when proving bottom-up (backwards). Note that this value is set to the current justification’s reference if there is already a justification. If blank, any label may be used as the justification reference (and the system will try them all in the process of searching). This setting does not affect other levels (depths) of the proof.

Search depth: How deep the search is to go. Use of a single axiom or theorem is depth 1, a statement that requires a depth 1 search on a depth 1 search is depth 2, and so on. The default search depth value is 4. Larger numbers enable more automation but generally take exponentially more time.

Length restriction: This setting restricts what justifications are considered based on their length. This is a simple heuristic that, when used, can significantly speed up search. This setting is not applied to the first depth of the search, only to deeper levels, so it has no effect on searches with search depth 1. This setting can limit justifications to be considered based on whether or not they are less than the length (or less than or equal to the length) of the statement being justified. In many cases longer statements shouldn’t be considered at deeper depths, since that often implies increasing instead of decreasing complexity. Let’s imagine that the system is searching and has to search more than depth 1. It is currently searching to see if it can use jA, and is in turn working to determine if it will try to prove justification jB to support jA (that is, jA might depend on jB). A value of “Less” means that the system will only consider justification jB if its length is less than justification jA. A value of “LessEq” means that the system will only consider jB if its length is less than or equal to jA. A value of “No” means the system will not restrict anything; this is the most flexible (it can find more proofs) but may take much longer.

Checkbox Allow new disjoints: Allow the addition of new disjoints.

Checkbox Allow new steps: Allow the addition of new steps.

Checkbox Allow new variables: Allow the addition of new variables.

Logging level (0..2): If you select a log level beyond 0, then information will be recorded, which can be helpful for debugging. You may find this information helpful in modifying the search options further. If such information is recorded, a “show proof tree” button appears in the results of the bottom-up prover once it’s stopped. You can then explore the proof tree and see what the prover found. In particular, you may find that the prover found a statement that “almost” worked, and then modify the search criteria further. If the logging level is 1 or more, you may enter the maximum number of branches, which will limit the number of branches checked. In many cases you will want to enter the maximum number of branches to prevent the logging from becoming overwhelming. Warning: Enabling logging (beyond log level 0) consumes significant memory and slows the search, especially for logging level 2. If you set logging level 2, you should restrict it such as by setting the label or setting the maximum number of branches.

You can speed up searches by not allowing new disjoints, new steps, and/or new variables, but in some cases this may mean a proof won’t be found.

This dialogue can be used to implement functions similar to certain functions of the mmj2 tool:

• In mmj2 you can select a specific set of steps that must be used in a justification of a given statement. You can do something similar by doing a bottom-up proof of that given statement, and selecting just those steps to be used as root steps at the “first level”. This can be quite similar to mmj2 if you also uncheck “allow new steps”, which will prevent the introduction of new steps.
• In mmj2 you can state that a specific axiom or theorem must be used as the justification. You can do the same by selecting it as the “Label” in a bottom-up proof.

Unification

Metamath-lamp’s current unification algorithm is only unidirectional, that is, it can only substitute in one direction to find a match. In the technical literature this algorithm is often described as “matching” as compared to full syntactic unification. This is in contrast to other tools, like mmj2, which implement full syntactic unification.

There are some discussions about removing this limitation in metamath-lamp. There’s nothing fundamental to metamath-lamp about this limitation; the issue is that it takes time to write a performant implementation of unification. We hope that future versions of the tool will remove this limitation. However, current users must work around this limitation.

Settings tab

The “Settings” tab lets you configure metamath-lamp to your liking.

You must press on “Apply Changes” for changes to be applied. Any changes you make in the Settings tab are not applied until you select “Apply Changes”. If you want to discard changes, select “Discard Changes”.

One setting in particular that you might want to change involves how to interpret left click. Should you edit statements with a click or a long-click? The choice is yours. By default, editing statements uses a long-click.

Most of the other settings should be fairly obvious, and in most cases you won’t want to change them.

If you don’t see the name of a database in the context dropdown, open the settings tab and check your settings. You may need to click on “Restore default URLs” and “apply changes”.

Explorer tab

The explorer view lets you see the various assertions (axioms and theorems) in the loaded database(s).

The top of the explorer view lets you select what to view; by default all assertions are included. You can select the assertion type (axioms, theorems or all), text that must be included in the label, or a pattern that must be in the conclusion (see search patterns). The crossed-out funnel symbol erases all search criteria, once again showing all assertions.

There are typically many assertions, so this is a paged view. Click on “<” and “>” to see the previous and next page, the page number to see a page, or enter the page number.

After that begin the list of assertions (theorems and axioms). Each assertion shows its count, the type of assertion (theorem or axiom), and the assertion label in bold. The rest of the display shows a list of 0 or more hypotheses, each prefixed with large black circle “⬤”. The final line of an assertion states what can be concluded via this assertion when its hypotheses are true.

You can use the fragment selector to copy useful portions of any statement. Next to the name of each axiom or theorem is a “>” symbol which lets you expand or hide its description.

If you select the label of an assertion, you will be brought to an individual assertion tab specific to that assertion. This tab will be dynamically created if it doesn’t exist already.

Individual Assertion tab

The tab bar shows all the opened dynamically-created individual assertions. You can click on the “x” after any dynamically-created tab to remove the tab.

Each individual assertion tab displays information about one assertion, including its description and proof.

Again, you can use the fragment selector to copy useful portions of any statement.

If it’s a theorem, you can select “show types”, which shows the proof that a given expression has the given correct types. If it’s an axiom, types are always shown (axioms are accepted as givens so there’s nothing else to prove). Metamath proofs include proofs of the types of each expression; you can decide whether or not to see this.

Clicking on a use of a hypothesis step label will show the individual assertion tab for that label (creating the tab if necessary).

At the beginning of the statement is a small “+” (reveal/hide), where you can reveal or hide a visualization of that step.

Clicking on a reference to an assertion will show an individual assertion tab of that assertion (creating the tab if necessary). That tab will provide detailed information about the assertion.

Temporary mode (TEMP mode)

You can load a pre-existing state by adding ?editorState=... to the end of the URL (use “Export to URL” to generate these URLs)..

When you load in such URLs, Metamath-lamp is opened in temporary mode (aka TEMP mode). Changes in temporary mode will not be stored in the editor’s content to the local storage.

To reduce the risk of accidentally doing something important while in temporary mode, word “Editor” is shaded orange (warning you that editing is temporary) and the web page header starts with “TEMP”. Also, the first attempt to edit will remind you that you’re in temporary mode and that changes will be discarded later.

Common set.mm symbols

Here are some common symbols defined in set.mm.

Symbols for variables

• A, B, C, and any other uppercase Latin letter is a variable that represents an arbitrary expression of a class. All sets are classes, not all classes are sets. By convention we start with A unless there’s a reason to do otherwise.
• ph, ps, and ch represent the Greek letters φ, ψ, and χ. Lowercase Greek letters represent an arbitrary expression with a value of either true or false.
• x, y, z, and other lowercase Latin letters represent a set variable.

Logical operators

• -> represents “implies”. The left-hand-side of an implication is called the antecedent; the right-hand-side of an implication is called the consequent.
• -. means logical not; if what follows is true then the result is false, if what follows is false then the result is true.
• \/ represents logical “and”. If both sides of it are true then the result is true (otherwise it’s false).
• /\ represents logical “or”. If either side of it is true then the result is true (otherwise it’s false).

Relations

• = represents “is equal to”; the left and right sides must be classes.
• =/= represents “not equal to”.
• e. represents “is a member of”; so A e. B is how we write “A ∈ B”. The expression A e. CC means “A is a complex number”.

Other symbols

• CC represents the set of all complex numbers.
• / represents complex number division.
• The form ( FUNCTION ` ARGUMENT ) applies function FUNCTION to ARGUMENT, that is, it determines the value of the function for that argument. Therefore ( tan ` A ) is the tangent of A. This left apostrophe notation originated from Peano and was adopted in Principia Mathematica by Whitehead and Russell, Quine, and others. This notation means the same thing as the tan(A) notation used by others but without context-dependent notational ambiguity.

JSON format

Metamath-lamp exports proofs in JSON format, which you can later import to restore the current state. We recommend using the .lamp.json extension if you store them in a file.

JSON format specification

The JSON format has a single object at its root, with the following keys and values:

• “srcs”: Array of source objects (see below). This array collectively defines the proof context.
• “descr”: String. The description.
• “varsText”: String. The text of the variables.
• “disjText”: String. The text of the disjunctions.
• “stmts”: Array of step objects (see below).

A source object has the following keys and values:

• “typ”: String. It should be “Web” (load from the web) or “Local”.
• “fileName”: String. The filename (if “typ” is “Local”).
• “url”: String. The URL (if “typ” is “Web”).
• “readInstr”: String. This can be “StopBefore”, “StopAfter”, or “ReadAll”.
• “label”: String. This is the label to “StopBefore” or “StopAfter”.
• “resetNestingLevel”: Boolean. If true, all the inner blocks are automatically closed. The result will be similar to the situation if immediately after this source was read there were closing $} added to match all already read and currently open blocks that were opened with ${. Blocks are defined in the Metamath book in “4.2.8 Scoping Statements”.
• “allLabels”: Optional empty Array. Internally this is not empty and is used to speed up some parts of the application. When exported to JSON this is always exported as an empty array. It is not required when importing from JSON; if you remove it, the import will still work.

A step object has the following keys and values:

• “label”: String. The label for this step. Every label should be unique in a proof. Labels for the goal and hypotheses should not have any other use in the context (it can’t be a symbol or label in use).
• “typ”: String. This is “e” for an (essential) hypothesis or “p” for a provable statement. Note that a goal statement has a “typ” of “p” with “isGoal” is set to true.
• “isGoal”: Boolean. This is true if this step is a goal, else it is false. There should be at most one step that is a goal.
• “cont”: String. This is the text of the step’s statement, including the prefix typecode (such as |-). E.g., “|- ( ph -> ps )” is an example of such a string,
• “jstfText”: String. This is the justification text. Note that the metamath-lamp tool will always show HYP for a step that is an essential hypothesis (“typ” of “e”), regardless of the value stored. If the justification text is not empty, it should be of the form HYPS : REF where HYPS is a space-separated sequence of zero or more step labels, and the REF is the label of a statement available in the context. There is normally a space on either side of the colon.

JSON Example

Here’s an example of the JSON format. Here’s the easy proof of syl:

Screenshot of syl (easy proof)

Here is the equivalent JSON for it:

{
  "srcs": [
    {
      "typ": "Web",
      "fileName": "",
      "url": "https://us.metamath.org/metamath/set.mm",
      "readInstr": "StopBefore",
      "label": "syl",
      "resetNestingLevel": true,
      "allLabels": []
    }
  ],
  "descr": "Reprove syllogism (\"syl\"), using only axioms.",
  "varsText": "",
  "disjText": "",
  "stmts": [
    {
      "label": "syl.1",
      "typ": "e",
      "isGoal": false,
      "cont": "|- ( ph -> ps )",
      "jstfText": ""
    },
    {
      "label": "syl.2",
      "typ": "e",
      "isGoal": false,
      "cont": "|- ( ps -> ch )",
      "jstfText": ""
    },
    {
      "label": "1",
      "typ": "p",
      "isGoal": false,
      "cont": "|- ( ( ph -> ps ) -> ( ph -> ch ) )",
      "jstfText": "syl.2 : imim2i"
    },
    {
      "label": "syl",
      "typ": "p",
      "isGoal": true,
      "cont": "|- ( ph -> ch )",
      "jstfText": "syl.1 1 : ax-mp"
    }
  ]
}

Metamath-lamp update history

Version 11

Major additions in version 11:

• Added an “explorer tab” and dynamic tabs for existing proofs, enabling users to examine the current context at any time.
• Works well on smartphones (e.g., supports “long-click” or “long-tap”).
• More unified UI - all edits by default use a “long-click”.
• Supports identifying one provable statement as the “goal statement” and treats it specially, making the UI easier to use.
• Visualization can be enabled or disabled per justification.
• More control over which fields are displayed during editing.

Future directions

There are many ways the metamath-lamp tool could be expanded. Proposals are listed in its issues and proposed changes are listed in its pull requests. You can follow commits in its develop branch and even try out the development version of metamath-lamp application page (but this may not work as expected).

Here are some likely future capabilities:

• In the editor, click on a reference in a justification to view its details in a different dynamic tab
• Use a full unification algorithm
• Undo/redo
• Some automation
• Ensuring that statements marked discouraged are not automatically added by default and syntax marked discouraged are ignored by default

One planned new capability is paste in the fragment selector:

Icon	Meaning	Visual Description	Additional information
paste	Paste	Clipboard	Paste the clipboard contents onto the current selected fragment

In the statement fragment selector icon bar, the icon paste (paste) will paste the clipboard’s current contents onto the current selected fragment. The expected use is that you’ll select a fragment in one area, click on the icon copy (copy to clipboard), select another fragment you want to replace, and then click on the icon paste (paste). Copy and paste work well within the application, however, note that the browser may request additional permissions if you try to paste data from outside the current application. NB: In Firefox copy to clipboard works as expected, but the icon paste (paste) will currently only paste from the current metamath-lamp application, and never from a different browser origin or a different application.

Here are proposed v12 milestones.

Help, feedback, and contributions

Metamath-lamp is intended to be an easy-to-use proof assistant. We hope you’ll find that it meets your needs.

No matter how you decide to contribute, we thank you for your time.

Creating and contributing proofs

As noted earlier, if you want to run the metamath-lamp application to create proofs, view the Metamath-lamp application page<

If you need help on how to create Metamath proofs, or on how to use the metamath-lamp tool to create Metamath proofs, the best place to go is the Metamath mailing list. You can find a lot of general information about Metamath at the Metamath home page.

If you’re making a contribution to a Metamath database, such as a new proof, please contribute those as changes to the database’s repository. For example, for set.mm, propose changes to the set.mm database source repository. If it’s your first time, you should contact the mailing list; they would be delighted to help you complete that process.

Feedback on this guide (not the metamath-lamp tool)

If you have feedback (issues) or contributions (pull requests) for this guide, please do that by filing issues and pull requests on the Metamath-lamp guide source markdown repository. Do not send proposals about the tool to this repo, as it is only for proposed changes to this guide document.

Feedback on the metamath-lamp tool (not the guide)

For feedback or proposed changes to the Metamath-lamp tool itself, please file issues or create pull requests against the metamath-lamp source code repository. Do not send proposals about the guide to this repo, as it is only for proposed changes to the tool itself

If you want to be on the bleeding edge, you can use the development version of Metamath-lamp application page (but this may not work as expected).

Quick tour of the metamath-lamp source code

If you wish to try to contribute code to the metamath-lamp project itself, you’ll need to learn more. Here are some hints.

The metamath-lamp program is written in the ReScript programming language. ReScript is a robustly typed language that compiles to efficient and human-readable JavaScript. ReScript is a programming language similar to OCaml; it is multi-paradigm but it encourages functional programming approaches. ReScript source files have the extension .res (for most code) or .resi (for external interfaces).

For more about ReScript, see this introduction and overview. ReScript has a sound type system and its code has no null/undefined errors. By default you must specify the full scoped name of a function, e.g., mytext->Js_string2.split(":").

Metamath-lamp uses the widely-used React library to implement its user interface. The ReScript programming language comes with a robust API to use React and JavaScript.

In discussions, metamath-lamp is often abbreviated as mm-lamp.

To simplify things and not have to think about different possible scenarios, metamath-lamp tends to use the approach “stop if bad data is detected and let the user decide how to correct the data”.

Here are some conventions for the source code filenames:

• Filenames beginning with MM_cmp_*.res (meaning “component”) are very coupled with UI related things, e.g., React, the web browser DOM, window global variables, and so on. Usually one cmp file contains one React component, but this is not a strict rule and there are a few exceptions.
• Filenames beginning with MM_wrk_*.res (meaning “worker”) must not depend on UI related things, as these files could be (eventually) used in a worker thread. Worker threads don’t support many features which are supported in the main thread. If such a UI related feature appears in a worker thread it usually leads to an error (compilation or runtime). Where possible, put functionality in MM_wrk_ files instead of MM_cmp_ files; this means they could be called in worker threads and makes them much easier to test.

Here are some conventions for the source code itself:

1. Where at all possible, please reuse existing functions unless there’s a strong reason to do otherwise, as this simplifies code review. It’s acknowledged that this is a challenge when you are new to the code base.
2. Functional style is generally used, e.g., filter and map.
3. Like several other languages, many functions return an Option (which can be Some('a) or None) or a Result (which can be Ok('good) or Error('bad)). These enable compile-time checking that prevent null and undefined errors. By convention prefer using these for returning error information. ReScript also supports exceptions, but you should generally avoid using exceptions for control flow unless they’re needed.
4. Names normally use camelCase. Most names (including variable and function names) use lowerCamelCase, but module names use UpperCamelCase.
5. ReScript has two built-in libraries: Js for simple interfaces direct to JavaScript, and Belt which provides more sophisticated collection handling. When either works, prefer the Js interfaces which are simpler and map directly to JavaScript, but do use Belt when it helps.

6. Use the -> (pipe) construct as is now conventional in ReScript, especially in a function chain. The -> is syntactic sugar that allows you to call a function but with the parameter to the left of -> becoming the first (or specified) parameter of the function. For example:

   Expression	Means
   myData->MyModule.myFunction	MyModule.myFunction(myData)
   myData->MyModule.myFunction(fooData)	MyModule.myfunction(myData, fooData)
   myData->MyModule.myFunction(fooData, _)	MyModule.myfunction(fooData, myData)

   See ReScript pipe for more information. This implies preferring the newer “data-first” ReScript interfaces, for example, you should prefer Array2 over Array. Please note that using the pipe construct is not obligatory if you want to contribute to the codebase - you may still use conventional function application like func(arg1, arg2) if you prefer. However, during the pull request review, you may be asked to use the pipe construct in some places, especially where there are function chains (deeply nested function calls). For example, instead of func1(func2(func3(arg))) the preferred construct is arg->func3->func2->func1.

7. If you add/modify functionality, please add/modify tests. The source code for tests is in *_test.res files. RSpec-style tests are created using describe({... it({... )} ..}).

Licensing

You may use, modify, and share this guide under the terms of either the MIT license or the Creative Commons Attribution 4.0 International (CC-BY-4.0) license, at your choice.

In short, the license of this guide can be expressed using this SPDX license expression:

SPDX-License-Identifier: (MIT OR CC-BY-4.0)

We welcome contributions! Contributions back to this guide must be contributed under the same terms.

Metamath-lamp is licensed separately (it is released under the MIT license).

Detailed table of contents

Here is the detailed table of contents (ToC). We put this ToC near the end of the document so that readers using small screens won’t need to scroll through it just to see the early content.

• Quick start
• Sample Screenshot
• User guide (tutorial)
  • Proof: 2 + 2 = 4
    • Selecting the proof context for 2p2e4
    • Adjustments for small displays
    • Setting the goal statement for 2p2e4
    • Setting the goal label for 2p2e4
    • Setting the description for 2p2e4
    • Interlude: Brief review of metamath-lamp user interface
    • Deciding on a proof strategy for 2p2e4
    • Expanding the definition of 4
    • Using statement fragments to connect 3 + 1 with 4
    • Expanding the meaning of ( 2 + 2 )
    • Showing these expansions are equal
    • We have successfully proved that 2 + 2 = 4
    • Renumbering steps
    • Getting the completed proof
    • Exporting and importing your current state
    • Looking at proof steps
    • Visualization: a powerful metamath-lamp capability
    • Changing the order of steps
    • Another (easier) way
    • A brief discussions on settings
    • More tricks for small displays
  • A tour using the Explorer tab
    • Warning: Magic here
    • Loading a context for the explorer
    • Trying out the explorer tab
    • A few set.mm symbols
    • Viewing proof of mp2
    • Revealing types in the individual assertion tabs
    • Revealing more about Metamath types in the editor
    • Gaining an understanding of set.mm’s beginnings
      • Assertion 1: Theorem idi
      • Assertion 2: Theorem a1ii
      • Assertion 3: Syntax axiom wn
      • Assertion 4: Syntax axiom wi
      • Assertion 5: Axiom ax-mp (modus ponens)
      • Assertion 6: Axiom ax-1
      • Assertion 7: Axiom ax-2
      • Assertion 8: Axiom ax-3
      • Assertion 9: Theorem mp2
      • Going beyond
  • Proof: Principle of the syllogism (syl)
    • Setting up the context and goal step for syl
    • Setting up the description, goal, and hypotheses for syl
    • Starting situation for syl
    • Easy proof of syl
    • Hard mode: Proving syl using only axioms
      • Switch from our current state to hard mode
      • What axioms are available in this situation?
      • Working backwards on syl
      • Interlude: Work variables
      • Globally substituting some work variables
      • Handling the duplication in syl
      • Completing syl in hard mode
      • Screen shot of syl with only axioms
  • Proof: The reciprocal of the cotangent is tangent (reccot)
    • Selecting the proof context for reccot
    • Setting the goal for reccot
    • Deciding on a proof strategy for reccot
    • Beginning to expand the definition of tangent
    • Interlude: Work variables in reccot
    • Completing the work to expand the definition of tangent
    • Expanding the definition of cotangent
    • What does reciprocal do?
    • Matching the goal’s antecedent for tangent
    • Matching the goal’s antecedent for cotangent
    • Handling the reciprocal of the cotangent
    • Proving the preconditions we need
    • Exporting to URL and temporary mode (TEMP mode)
  • Creating your own examples from existing proofs
  • Loading existing metamath-lamp proofs
  • Notes about Metamath databases
  • Conclusion of this user guide
• Reference manual
  • Basic UI conventions
  • Loading source Metamath databases to create the proof context
  • Main tabs: Settings, Editor, and Explorer
  • Editor tab
    • Editor command icon bar
    • Fundamental proof information
      • Description
      • Work and Local Variables
      • Disjoints
    • List of steps in the proof
    • Fragment selectors
    • How to state the goal and hypotheses
    • Search patterns
    • Global substitution
    • Proving bottom-up
      • How bottom-up proving works
      • Proving bottom-up dialogue box options
    • Unification
  • Settings tab
  • Explorer tab
  • Individual Assertion tab
  • Temporary mode (TEMP mode)
  • Common set.mm symbols
    • Symbols for variables
    • Logical operators
    • Relations
    • Other symbols
  • JSON format
    • JSON format specification
    • JSON Example
  • Metamath-lamp update history
    • Version 11
• Future directions
• Help, feedback, and contributions
  • Creating and contributing proofs
  • Feedback on this guide (not the metamath-lamp tool)
  • Feedback on the metamath-lamp tool (not the guide)
  • Quick tour of the metamath-lamp source code
• Licensing
• Detailed table of contents
• Authors and Reviewers

Authors and Reviewers

This guide was written by David A. Wheeler (@david-a-wheeler) and reviewed by Igor Ieskov (@expln).

This site is open source. Improve this page.